こんにちは。コンテンツ部顧問のnoriです。
近年、僕が読んだSF小説で面白かったのは、「三体」(劉慈欣)と「あなたの人生の物語」(テッド・チャン)の作品でした。「三体」は現在、配信系サービスで映像化され、「あなたの人生の物語」は映画「メッセージ」として日本では2017年5月に公開されましたね。
SF小説、SF映画の中でよく「次元」の扱いが台詞に出てきたり、VFXの表現に使われています。ある種の浪漫がありますが、現在のSF作品は科学的考証もかなりの高いレベルで考証され作品に反映されています。我々だって言葉の意味については、少しは分かっていますが内容は難しいですよね。最近は「反重力は存在しない」ことも発表され、これの実証がこれから進んでいくと思いますが、これが立証されていくとドラえもんのタケコプターは使えないし、アイザック・アシモフのSF作品も数作は厳しいものとなります。科学は僕らの夢を叶えると同時に残酷に夢を潰していくものですね。
「三体」における11次元の内容に関して(感想)
11次元の領域を3次元から利用する
おそらく超弦理論からの設定でしょう。とても上手に設定・活用されていると思います。
次元空間はごく小さな要素の中に大半は閉じ込められていますから、実際の空間次元が11次元であるにもかかわらず、我々は3次元しか認識できないというような設定があり、智子という1個の陽子であるコンピュータは、この空間構造を活用しています。
外部からそれを確認した場合のスケールは小さくても、構造の次元が1つ上がるごとに、その内部で利用できる情報量はかなり増えていきます。三体の世界では、9次元までを操作する技術を有しています。この一連の開発話の中で、粒子すら、当然高次元を圧縮した、内部に凄まじい情報量、つまりは複雑性を実は持っているものと語られること。その内部には、それこそ複雑性が生み出すもの、生命体が存在していたりすることもある。その話を飛躍して解釈してしまうと、我々のこの世界までも、そういう折りたたまれた次元の中、つまり大きく見えて小さな世界かもしれないという発想もありうるでしょう。作中で、粒子同士の崩壊現象の度に、そのような小宇宙は壊れてしまっているという例の通り、この宇宙も突然に崩壊してしまうということもありえるかしれないと想像すると・・・。面白いSF小説ですね。
さて、
小学生では平面(2次元)や立体(3次元)のモデルが出てきますし、中学生、高校生では座標軸を与えられてもう少し論理的に学習していきますが、数学と物理学では少し「次元」の扱いが異なるので注意も必要です。
まずはそこから振り返りをしながら11次元の世界を少し覗いてみましょう!!
【次元】の基本的な意味
数学において、
「次元」は「ある空間がどのように広がっているのか」を示すために使用する概念です。座標を数値で示すことにより、特定の位置を指し示すことができます。立体や空間は直行する3方向の座標(縦・横・高さ)によって示すことができます。つまり立体や空間は「3次元」であることになますね。
ところが物理学の世界になると少し扱いが異なります。
「次元」と「単位」の違い
物理学において、「次元」は「単位」と混同されやすいので注意が必要です。
「単位」とは、計測する際の基準としてあらかじめ定められた特定の量、および、その呼び名のことです。
基本的には、「長さ」の単位は「メートル(m)」、「重さ」の単位は「キログラム(kg)」、「時間」の単位は「秒(s)」が用いられます。
ところが、
「次元」とは、各種の単位によって示される概念を種類または性質ごとに総合した概念である。「メートル」や「秒」といった具体的な単位ではなく、「長さ(L)」「時間(T)」といった抽象的な括りが「次元」なのです。
「単位」は一様ではなく、さまざまな種類があります。たとえば長さの単位なら「cm」や「km」、あるいは「yd(ヤード)」「ft(フィート)」などの単位があます。これらは、いずれも「長さの単位」です。そして、その「長さ」という概念そのものが「次元」なのです。
式においては「長さ」は「L」、「重さ」は「M」、「時間」は「T」の記号で表されます。
【11次元(超弦理論による次数・次元の世界)】
1、2、3と順に10まで足した合計は? 足し算を繰り返してもよいのですが、簡単な計算方法を子供の頃に考えた人は多いでしょう。気がつけば簡単です。
1+10=11、2+9=11、のように足すと11になる数字の組が5個あるので、11×5=55
になります。簡単ですよね。では、これが10ではなく無限大だとどうなるでしょうか?。
実は我々が数えられる有限の場合の方法・考えが単純には使えないのです。
この答えは驚くべきことに
-1/12
になると、18世紀の数学者、オイラーが複素数の解析学を用いて導き出しました。
普通に考えれば、1+2+3+4+・・・・=∞になるかと思いきやそうはならないのです。これが、数学における有限(数が数えられる)と無限の扱いの違いなのです。
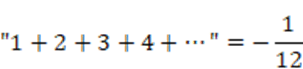
何故か?不思議なことに間違えた論証でも何故か計算結果がでます(笑)。
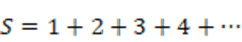
これだと際限がないので計算結果は「無限」と思うか「分からない」になりますね。そこに次の式を考えてみます(交代級数といいます)。
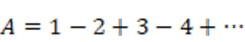
次に引き算を行うと
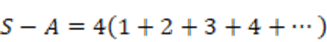
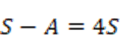
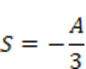
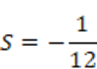
しかし、この級数の最終項の極限はゼロではありません。収束(一定の値に近づく)しないのに収束した結果が出てしまうのです(笑&怪我の功名)。そのため、上記の計算方法は正しくありませんがとりあえず答えは出てきます(笑)。
そこで以下の性質を利用します。
減衰振動は、発散級数を収束させます(詳細は省略します。そういうものだと考えて下さい)そのため、減衰振動は自然数の等比級数を収束できるかもしれないという発想です。
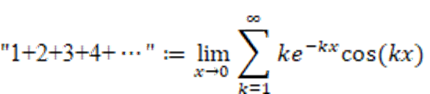
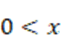
これを計算すると(これも計算は省略します)、
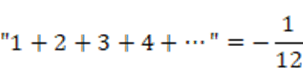
が得られます。
これが、今回の数字「11次元」を導き出す重要な小道具になります。
この「次元」とは何か。
「1点の位置を決めるのに必要な数値の個数」という説明がわかりやすと思います。1次元は直線の世界で、原点からの距離だけで位置は決まります。2次元は平面で縦と横の2個の、3次元ならそれに高さを加えた3個の数値があれば良いのです。
我々が住んでいる空間は3次元、時間を加えると4次元の時空間とされます。でも5次元以上は途端に見当がつかなくなります。
そんな世界を提示するのが、宇宙の究極の成り立ちを探る「超ひも理論」あるいは「超弦理論」と呼ばれるものです。
物質の細部を見ていくと、原子、原子核、素粒子と新たな粒子が現れてきます。その先には、1種類の極微の「弦(ひも)」があると考えるのがその名の由来です。弦が様々な振動をすることで、多種多様な素粒子が現れる。そして弦の振動は1、2、3倍…と整数倍になる。振動はエネルギーでもあり、すなわち質量にも結びつきます。
これを超ひも理論で光子の質量を求める式に当てはめてみます。途中の過程については膨大な理論や式等々が必要となるので省きますが、最終的な式は、
2+(次元数-1)×(1+2+3+・・・・)×3=0
と表せます。(1+2+3+…)は、振動数を表す部分です。ここに先程得られたのオイラーの答え「-1/12」を代入します。光子の質量(右辺)は0(ゼロ)なので、次元数は9になることが導かれます。
でも現実の世界は3次元。残りの6次元はどこにあるのでしょうか?。
例えとして使われるのが綱渡りを考えてみましょう。綱渡りをする人には、綱は前か後ろにしか進めない1次元の世界。でも綱の上を這うアリがいたら、アリは前後左右と平面のように動ける2次元の世界と認識するでしょう。つまりアリの見ている平面は綱渡りをしている人には隠されているということになりますね。
つまり、残りの6次元の空間は、極めて小さくなっていて、認識はできないけれど、この3次元空間の中に畳み込まれている。都合の良いつじつま合わせに聞こえますが、きちんと数学的に示される考えです。
この超弦理論の9次元は、弦と弦の間に働く力が強くなった特殊な場合には、次元が1つ増えて10次元に。そして時間を足して11次元の時空間になるのです。
空間が増えたり減ったりするなんて、想像の彼方ですよね!!
超弦理論はまだ理論の段階で、実験で確かめられるのはずっと先だと思います。でも100年前にアインシュタインが生み出した相対性理論が、今では全地球測位システム(GPS)の正確性を保つのに欠かせないように、超弦理論もいつか実際の技術と結びつくかもしれません。
背景を少し知ろう!
とは言っても11次元の世界にたどり着くまでの歴史的な背景も少しは知っておくと面白いと思います。関心のある人は調べてみると新しい世界と出会えると思います。
注意:以下の文は厳密に理解する必要はありません。こんなものか~、何言ってるのか分からない~!、難しい~!、わけわんない!!等々・・・、その程度で良いと思います。現代理論物理学は現代数学の理解も必要となるので難しい数式となり、高校程度の数学では厳しいのです。それ故、数式等々はあえて掲載していません(それでも必要な数式は掲載しました)。なるべく文字だけで説明しようと努力しましたが、正直な話、数式がないと厳しい面も多々ありました。その点はご了承下さい。本来はその説明をするための数式であり、それを利用して会話をしながら探求していくことが何よりも楽しいのですが(笑)。
歴史的な背景
19世紀後半の時代、一般に物理学というのは、もうほとんどパラダイムシフト(革命的な新事実の発見)など起こりえない、どころか解決すべき難題すらほとんど残されていないような分野だとされていました。
かつて、それ自体は不変的にただ存在している空間。ただ刻一刻とすぎるだけの不変的な時間。それら絶対的な時間と空間の中で、物質に働くニュートン力学(Newtonian mechanics)、そして空間内に広がる特殊物質エーテル(ether)と、それを媒体にして伝わる電磁気(Electromagnetism)の波(電磁波(Electromagnetic waves))の世界でした。
たったこれだけの要素で世界のどんな現象も説明できる単純で、理解しやすい世界だったのです。
そして物理学者に残されていた重要な課題は、ほぼ全てが理解されているような時代において、いまだ成されていなかった、エーテルなるものの確認のみのはずでした。
だがその探求が物理学時代の終演ではなく、始まりとなるのでした。
光速度cを観測する時
光というのは電磁波と同じ(つまり水と氷みたいなもの、状態が違うだけ)だと、マクスウェル(James Clerk Maxwell。1831~1879)という人が説きました。
彼はまた光の速度を(約)秒速30万キロほどだと示しました。それだけなら別になんて事もなかった。問題は、この「光速度(speed of light)」というのが、どんな観測者のどんな状況にも左右されない絶対的なものである事(マクスウェルの計算は、観測者の運動状態に依存しない)という事でした。
ようするに光速度というのは、例えば質量や温度といった、空間の中で方向を持たない(方向に影響を受けない)、いわゆる「スカラー(scalar)」と呼ばれる量(方向を持つ量がベクトル)なのですが、世界の何を基準にした見方も、その速度に影響与えない訳です。(厳密には、光は波としての速度は、その場の環境によって(見かけ上)変化します)
つまり光速度c(秒速30万キロ)は、観測者がどう動いてようと、cより速くも遅くも観測されない。これは、十九世紀までの物理学の知識がすべてである人たちには仰天する結果でした。隣で同じ方向に進んでいるものが止まって見えるのは当たり前のことでした。あなたが動いている車の中で座っている時、隣に人がいても、その人が車の速度で動いているようには見えないはずです。
エーテル確認されず
マクスウェルの計算が示した、光速度の普遍性という事実は、光という波の媒体と考えられていた、エーテルなるものを捉えるための実験によっても、証明されました。
この地球という星は太陽の周りを常に動いている。
そしてこの宇宙にエーテルが満ちているなら、地球の動きに影響を受けているはずです。水中でボールが動くと、水が影響を受けるように考えると分かりやすいと思います。
仮にエーテル自体が、観測不可能な(実際にそう考えられていた)機構なのだとしても、エーテルを媒体とした波である光(つまり電磁波)は観測出来はずです。一方向へと動く地球の上で、いくつかの方向から同じ距離を進む光の、方向に応じた相対的速度を計り、それらの相対的速度のズレ具合から、エーテルが地球に対し、どのような動きをしているのかがわかるはず。でもどんな精密な実験でも、地球の動きに対する光の相対的速度はズレませんでした。つまり、やはり光速度は絶対的なものだったのです。
後(1905年)にアインシュタイン(Albert Einstein。1879~1955)が、「エーテルなど必要なかった」と説き、その方向性が正しかったと受け入れられましたでも エーテルを観測できなかった最も有名な実験である「マイケルソン・モーリーの実験(Michelson-Morley experiment)の頃(1887年)には、「エーテルは地球を常に中心とし、地球上の観測者が常に光を同じ速度で観測してしまうよう、宇宙システム全体として調整されている」というような無茶な仮説もあったらしいのです。理論物理学の面白い所ですね。
原子に内部構造?
本来は物質構成の最小要素であったはずの原子の内部構造がはっきりと明らかになりだしたのも、19世紀と20世紀の境目くらいからです。
まず原子が崩壊するという事が明らかとなり、さらに、原子とは別物だとも考えられていた「電子(Electron)」が、原子内部に潜んでいる可能性も示唆され始められました。
最終的に物理学者たちは、「陽子(proton)」と「中性子(neutron)」とで成る「原子核(Nucleus)」と、その周囲を漂う「電子の雲」という原子の内部構造モデルを構築しました。
だが漂う電子の雲とはどういう事か?
電子はたったひとつでも、複数個でも、それを形成するのです。もちろん文字通りの雲ではなく、それはいわば「存在確率の波動」などと表現されたりします。容易には理解しがたい全然分からないものですね。もちろん、いきなりこんな奇妙なモデルが提唱されたわけでもありません。
存在確率の広がりというのは、それの数学的モデルに利用されている、不確定的な要素の実際的な解釈とされます。言うまでもありませんが、そのようなものを明確に観測できた例もありません。そこで、奇妙なのはこの宇宙ではなく、我々の使っている数学という不完全なツールの方という見方もあります。例えば、有限と無限の境目は未だに不明なのです。
なぜ電子はさっさと(回転(?))エネルギーを失い、反対の電荷を持つ(電磁気学的には、マイナスの電荷を持つ電子は、プラスの電荷を持つ原子核と引き合うはずです)原子核に落ちてくっついてしまわないのか?
という疑問に対して上手い解答を返すための苦心の結果が電子の雲モデルなのです。
光に関する更なる謎
光の奇妙さは、その絶対的速度だけではなかった
金属などに光をぶつけると、電子が放出される「光電効果(Photoelectric effect)」という現象がありますが、これは、金属原子などが、内部の原子核と電子の結びつきが弱いために、光のエネルギーによって弾き出されるために起こるとされていました。
そして波の道筋というのは、周期的に曲がりくねり、その瞬間、瞬間に少しずつ上下に方向を変え、連続した山と谷を作る。波が作る、そうした連続した山と谷の中で、隣り合う山と山の間の距離を「波長(wavelength)」といいますが、当然、光も波(電磁波)と考えられるので、その波長なるものを定義できます。
奇妙なのは、光電効果が起きる際に、光量を増やしても(つまり光を明るくしても)金属から弾きだされる電子の数が増えるだけで、電子が弾き出される勢いは強くなりません。しかし波長を変えれば、電子が弾き出される勢いが強くなったり、あるいは弱くなったりすることなのです。
具体的には、波長が短くなるほどに、電子は力強く弾き出されます。
何よりもおかしいと思われたのは、ある波長以上になった光は、もうどれだけ量を増やしても、光電効果をいっさい起こさなくなってしまう事なのです。
モノはエネルギーを持つ、当然光もです。そしてモノの量を増やせば、当然エネルギー(の総量)も増えるはずです。しかし、光はどれだけ量を増やそうともエネルギーが増えないらしいのです。それどころか、ある波長以上の光は、エネルギーを持たないのかもしれないです。誰もが知るように、0がいくらあっても0のままですものね。
波長の長い光がエネルギーを持たないものが、明らかにおかしい結論なのは、ストーブで暖まった経験がある人なら理解しやすです。我々は波長の領域により光を分類してますが、ストーブは、比較的長い波長の「赤外線(infrared ray)」という光を発します。赤外線は波長が長く、光電効果的にはエネルギーが大したことないように思えますが、ストーブの間近で、それが発する大量の赤外線を浴びれば、(たいていの人の基準で)相当に熱いですよね。
あの熱を生んでいるのがエネルギーでないのであれば何なのか?
一方、波長の短い光としては、太陽から降り注ぐ「紫外線(Ultraviolet rays)」がよく知られています。紫外線も近くで大量に浴びれば危険でしょう。でも雲に遮られた太陽が、なんとか届けてくれるわずかな紫外線なんて全然大した事ないみたいに思えます。
しかし、そんなわずかな紫外線でも光電効果によって、(数はわずかでも)電子に強烈な衝撃を与えるらしいのです。
大量の赤外線のエネルギーは本当に僅かな紫外線に負けているのでしょうか? 光電効果で飛ばされる電子の勢いを参考にするなら、明らかに負けています。でも、おかしいでしょう。
万有引力の定理、静かな崩壊
19世紀末期から20世紀初期。物理学者たちはエーテルを見つけようとしましたが、見つけられず、代わりに自分たちがいかに無知であったかを思い知らされました。ここまでに紹介したもの以外にも、数多くの既存理解の崩壊がありました。極端なのも、静かに地味に壊れた考えもあります。
「万有引力の定理(law of universal gravitation)」は、多分静かな崩壊といえます。
人類史上、最も偉大な発見のひとつとされ、数百年以上にわたり、科学者たちに崇められてきた、今だって使われる(使える)学校で教わった単純な数式です。
万有引力の公式
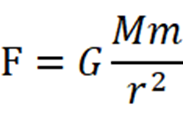
質量と質量が引き合う強さを述べたこの数式は、地球の重力の強さ(それからの脱出速度)や、惑星の動きなど、この世界で見られる多くの現象を上手く説明しました。だからこそ、この定理のみでは説明出来ない現象をどう考えればよいかは意見が割れました。
万有引力の定理で(もちろん無視できない余計な要素が多すぎた場合などではなく)予測出来なかった現象として代表的なのは、「水星の近日点移動(Mercury’s perihelion shift)」でしょう。
これは太陽の周りを巡る水星が、一周ごとに、太陽に最も近づく位置を変えていく現象です。この水星の近日点移動に関しては、周囲に(太陽と水星に比べれば)大きな質量もなく、運動エネルギーを奪う摩擦を生じさせるものもないので、近日点がどのように変化していくのかを万有引力の定理で予測するのは容易いはずでした。
ところが万有引力の定理を用いて予測した水星の近日点の変化経路は、実際のそれとズレてしまうのです。それが意味する所は明らかでした。
つまり、万有引力の定理は、不完全な理論だったのです。
そして20世紀へ
光の絶対的速度。原子よりさらに深く、小さな基本要素の存在。光電効果の謎。そして間違いなく完全ではない万有引力の定理。19世紀の物理学者たちは、自分たちは全てを知りつつあると自覚しながら、大量の問題を残してくれました。
そして20世紀になって、相対性理論と量子力学が登場しました。
アインシュタインの相対性理論
光がなぜ絶対的な速度を持っているのかを、誰もが納得出来るレベルで説明してみせたのがアインシュタインでした。
アインシュタインは、光の速度に関する性質を説明するための最初の一歩として、まずエーテルを捨てたことです。
アインシュタイン以前の研究者たちは、「確認こそされてないがエーテルは確かに存在している」という考えに囚われすぎていたかもしれないのです。だが実際は、エーテルにどんな新機能を考えることよりも、上手に光の速度に関する謎について全てを解決しました。
今では「特殊相対性理論」という名で知られるその理論では、まずこの世界を四次元と考える。だが縦、横、奥行き、明らかに空間は三次元であるということです。
第四の次元として当てられたのは、基本的にはそういうものでないと考えられてきた、「時間」です。そうして、それまではそれぞれに全く別の概念とされていた空間と時間は1つとされ、「時空」と呼ばれるようになりました。
そして当時、空間に対して、そういう事が起こるかもしれないと考えられていた「ローレンツ収縮(Lorentz contraction)」なる現象。つまり「運動する物体は、静止しているか、より遅い運動を行う観測者から見たら縮む」というこのローレンツ収縮を、単に空間を動く物体にでなく、個々の物体ごとが、個々に認識する時空に適用すれば、問題は解決するのです。つまり相対的だったのは光の速度でなく、時間と空間だったのでした。
例えばあなたが、友達の前を、光速にかなり近い速度で走ったとする。静止している友達にはローレンツ収縮により、あなたが縮んで見える。しかし当然、走っているあなた自身には、自分の姿が縮んで見えてはいない。ここで光速に近いが、それよりは遅いあなたを、さらに光が横切る場合を考えてみればよいのです。
速度というのは、対象の速度をv、ある時間をt、ある時間tの間に移動した距離をdとして
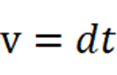
という式で求められる数値です。
普通に考えるなら、あなたの視点と、友達の視点にて、(あなたの体の長さが違っているなら)あなたを追い越す光が進まなければならない距離は、あなたと友達の視点によって違っています。すると友達とあなた、それぞれが計測する光の速度は違っているはずです。
しかし、光の速度は、誰がどういう状況で観測しようと変わらない。矛盾をなんとかするには、ローレンツ収縮を時間にまで適用するしかないでしょう。
友達が見るあなたの長さを0.1m、あなた自身が見るあなたの長さが0.5mだとして、さらに(簡単のために)光の速度を秒速0.5mだとする。あなたにとっての1秒が、友達にとっての5秒ならば(つまりあなたの時間がローレンツ収縮により縮んでいるなら)我々は公式より、当然、光速度を同じ値として計算するのです。
「時間が縮む」なんて考えなけれぱならないのは、そもそも空間にてローレンツ収縮が働くと仮定した場合にすぎません。でもそもそもローレンツ収縮を適用しなければ、「誰が観測しようと光速度は不変」だという事実を説明するのは難しいのです。
というわけで特殊相対性理論はかなり説得力がありましたが、実はそれだけではまだ駄目でした。
一般相対性理論
特殊相対性理論は、「光速に近づく者の時間が縮む」と示しているだけでありません。その計算結果から導かれる重要とされるふたつの結論があります。
ひとつが、有名な、
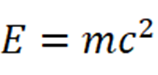
すなわち、質量とは実は姿を変えた(持った(?))エネルギーというものです。
そしてもうひとつが、「光速より速く加速する事は出来ない」という結論です。特殊相対性理論の計算式によると、何かが光速を越えて加速するのに必要なエネルギー数値は、無限なのです。無限とはもちろん、何よりも大きい数。
つまり加速するためにどれだけエネルギーを高めようとも、そのエネルギーは無限よりは小さい。よって光速を越える事ができない。
問題とは万有引力が瞬時に伝わるとされていた事でした。光速より速いはずがないのに(質量0の物質があるならどうかというと、おそらく光自体がそうであり、相対性理論的には質量0の物体は光速度で動くはずです。つまり質量0の何かすら光速度を超えることはありません。しかし例えば、この宇宙全体に、何かの情報が与えられた時に、その与えられた情報に合わせて機能するという重力システムがあるのだとしましょう。すると情報自体の質量が光速以上で移動可能と思われる値なら、この宇宙で重力は光速度以上で働くかもしれません。ではそのような質量値とは何かというと、普通に計算してみるなら虚数とされています)
こうして万有引力の定理と異なる、特殊相対性理論と矛盾なき新たな重力理論が必要となります。一般相対性理論はそのための、つまり新たな重力理論であったのです。
重力は加速
周囲に大きな天体(重力源)のない宇宙空間を、ロケットに乗って進む時、ロケットが十分勢いよく進んでいるなら、あなたの体はロケット内の壁に、まるである程度の重力があるかのように立てるでしょう。しかしロケットが停止すると、(元からだけど)いきなりの無重力状態で、あなたの体は宙に浮くと考えられます。
あなたは、地球の上に立ってるか、座ってるか、寝転んでいるかしてると思うけど、今、いきなり地球が跡形もなく消えてしまえば、やはり(今回は本当の意味で)いきなり無重力状態で、あなたは宙に浮くはずです。
これらは状況、原因は違えど、あなたが体感する経験は本質的に同じものなのです。アインシュタインはそう考えました。
そしてこれを「等価原理(equivalence principle)」と呼びました。
等価原理によると、ようするに重力は実は引力でなく、加速させる力となります。そして加速なので、十分に重力が強ければ、特殊相対性理論のような時間の縮みが発生します。逆に加速は、重力に引っ張られるのと同じなので、加速するモノは重くなります(質量(エネルギー)が増します)。でも重力はどのようにモノを加速させるのでしょうか?
時空の歪み

球体上などでの諸々を数学的に記述する、「リーマンの幾何学」(中学校の図形の証明を思い出して下さい)を実際の宇宙に適用して考えたなら、上手くいったのです。宇宙が球体上だとか考えるのではない。アインシュタインは、重力が時空間を曲げてしまうものだと想定したのです。重力の正体は時空間の歪みであり、加速するのは、曲がりくねった時空間を滑るためと。
質量は空間を歪ませる。そしてその歪みが広がる速度は光速度と同じだとして計算すると、万有引力の定理では出来なかった「水星の近日点移動の変化予測」もできました。当然そうなると、重力が伝わる速度は光速度と同じで、越えないということになり、一般相対性理論は、特殊相対性理論と矛盾はしません。
そうして、一般相対性理論もまた、かなり確からしいとなりましたが、今ではすっかり有名となった2つの奇妙な結論を生みます。
ビッグバンとブラックホール、それに特異点
どう数字を割り当てようとも、一般相対性理論の計算式をそのまま使えば、この宇宙は広がり続けるか、収縮しているかを続けます。この考えをそのまま受け入れ、宇宙は小さな点から広がる事で始まったという「ビッグバン理論」は誕生しました。
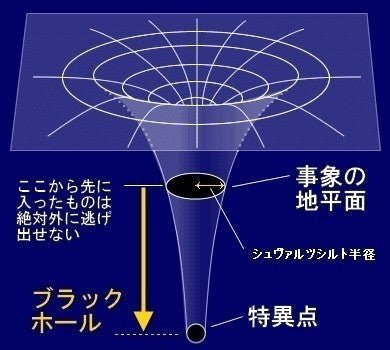
ビッグバンやブラックホールの何が問題なのかというと、ビッグバンは最初の点、ブラックホールはその中心の点である。「特異点(Gravitational singularity)」と呼ばれる、いくらかの質量が無限に収縮していく点です。
本当に2つの相対性理論が正しいのなら、確かに存在するはずの、その(名前通りに)特異な点をどう解釈すればよいのか? まともな解釈が出来るというなら、是非、お願いします。
特異点はまさに、「開かずの扉の先にいた不死身の怪物」みたいなものなのです。怪物を殺す事はどれほど難しいのか? 開かずの扉はやはり開けないまま、別のルートを探す方がよいのか?
量子力学
光速度に近づく時や、高重力場に関して相対性理論が解き明かしていったのと、ほぼ時を同じくして、原子以下の世界を記述する量子力学は誕生しました。
始まりはいつであったか? 少なくともプランク(Max Karl Ernst Ludwig Planck。1858~1947)の発想は、ごく初期でした。19世紀末期、プランクは密閉された空間内における電磁波の持つエネルギーの問題に取り組み、まったく予想外のとんでもない可能性を導いてしまうのです。
問題は、
密閉された空間内を熱した時、その空間内には熱に応じたエネルギーが発生します。アインシュタインが、質量はエネルギーなどと言い出す前から、光や電磁波はエネルギーだと考えられていたので、つまり密閉空間内には、光(電磁波)が発生する。その発生する光の強さを計算式で導こうとすると、従来のように光を波としていては上手くいかなかったのです。熱が高まり、エネルギーが増す時、エネルギーの波は様々なパターンを見せる。それら全てのエネルギー密度を計算したら、密閉空間内のエネルギーは無限だという結果が出てしまう。宇宙全体ならともかく、単に密閉された小さな空間内のエネルギーが無限だというのは何かおかしく思えるでしょう。そこでエネルギーは連続(アナログ)的なものでなく、物質が原子の塊であるように、何か小さな構成要素の塊だというアイデアをプランクは採用してみましたた。そうすると上手くいったのです。
例えばあるエネルギー領域について考える。右端が数字で1という弱いエネルギー。左端が数字で5という強い(?)エネルギー。この領域全体のエネルギー密度を考える場合、右端は1、左端が5だとして、後はその間のエネルギーを調べ、合計すればいいのです。
しかしエネルギーが連続的に変化するものならば、例えば1と5の間には2や3だけでなく、1.1とか2.0264312とか、無限の数字が存在する事となり、当然その全てのエネルギーを計算したら無限になってしまう。だがエネルギーが1の倍数の数字にしかならないとしたら、1と5の間のエネルギーは単に2、3、4しかなくなり、全エネルギー密度が無限になるのを回避できます。
つまり、エネルギーには最小単位があったのです。エネルギーが変化する時、その変化は不連続(デジタル)だったのです。エネルギーを数字で表す時、その値は必ず「プランク定数(Planck constant)」と呼ばれる数の整数倍となります。
光電効果の解明
プランクのアイデアに影響を受けたアインシュタインは、光を波でなく粒子とすれば、光電効果を説明できるとしました。
そもそも光電効果の問題は、光の量を増やしても、つまり総エネルギーを増やしても、弾き飛ばす電子の量を増やしはするのに、勢いは強くしない。そしてどういう訳だが、波長を短くすると、電子は強く弾き飛ばされるという事でした。でも光が波でありながら、実は粒子の集まりだとしたらどうだろうか。エネルギーを持つのは「光子(photon)」と名付けられた、その粒子ひとつひとつであり、そのエネルギーの強さが波長の短さとして我々に捉えられるのだとしたら、謎は解けます。
光、つまり光子の集まりが、鉄などに当たる時、不安定な電子に当たった光子は、それを弾き飛ばす。その強さは当然、光子ひとつひとつの抱えるエネルギー量(波長)に比例する。だから波長が短くなれば飛ばされる電子の勢いが増すのです。そして光量を、つまり光子の数を増やせば、当然、不安定な電子に当たる光子の数も増える。だから光量を増やすと飛ばされる電子の数は増すのです。
ある波長以上の光が、量をどれだけ増やそうと、光電効果を起こさない理由も今や明らかです。つまりその光を成す光子それぞれのエネルギーが電子を弾き飛ばせないほどに弱いのです。光子の数を増やせば、全体の総エネルギーは増す。しかし光子ひとつひとつが弱いので、いくら不安定な電子に個々で当たろうと、効果はないというわけです。
二重スリット実験
エネルギーの最小単位。そして波であるはずの光を構成する粒子は、いつしか「量子(quantum)」と呼ばれるようになりました。そしてさらに研究が進むと、原子以下の世界はこの量子なるもので構成されているという事がわかってきました。
例えば電子も量子のひとつとされた。現在、その内部構造が明らかとなっていない、最小要素候補は全て量子だとも言われてます。
量子は粒子であるように思われてます。それが集まって物理的な何かを形成するのだから。しかしまた量子は波の性質を持っている(これは集合体になると波の性質を持つようになるというわけではなく、単体の粒子ですでに波の性質を有する場合があるということ)。この事は、「二重スリット実験(Double-slit experiment)」という方法ではっきり確かめられています。
二重スリット実験に必要なのは、単体の電子(量子)の発射台と、電子を焼き付けるスクリーン。そして発射台とスクリーンの間に置かれた、二ヶ所にスリット(隙間)がある板となります。この実験はかつて、まだ電子を単体で放つ事が出来なかった時代に、光が波である事を証明するために提案されたものです。単体の電子でなく、光をスクリーンに向けて放つ。すると2つのスリットを潜った先にて、光はスクリーンに縞模様を映したのです。
仮に光が粒子(の集合体)であるなら、縞模様でなく、単に2つの模様がスクリーンに映されるはず。単純な考え方ですね。スリット2つのいずれかを、それぞれ潜った光の粒子は、それぞれがそのままその先に模様を作ります。でも光が波なら、スリットを潜った先で、それは広がり、重なった部分部分で(波というのはそういう性質があるので)打ち消しあい、結果、縞模様ができます。実際、そもそも光が波だとされた最大の証拠のひとつが、スリットの先で、光が縞模様を作るという実験結果でした。
でも単体の電子でこの実験をやればどうなるか? 電子をひとつ発射すると、スクリーンにはひとつの点が出来る。当たり前ですよね。しかし電子をさらに次々と放ち続けるとどうなっていくか? なんと、電子ひとつひとつは、最終的に縞模様を作るのです。
ひとつひとつ放たれた電子はどこにいる? 電子を放つと、それはスクリーンに到達する。その次も、その次も、どこかで波のような打ち消し合いが起こる。まるで電子が辿った経路の記録が、新たな電子の経路を打ち消しているかのように。
シュレーディンガー方程式の波動関数
量子の振る舞いを数学的に記述する最も一般的な式のひとつがシュレーディンガー方程式です。
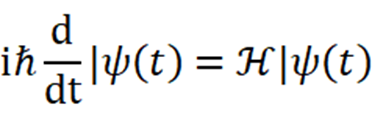
この数式で、i(虚数)が現れる原因は、実質的に数学側の仕様のせいであり、物理学的にはあまり関係ありません。
他は、ここでの議論に重要な「ψ(プサイ)」以外は、時間の変化とかエネルギーに関係してる部分であり、そんなに気にしなくてよいです。
問題は「波動関数(Wave function)」と呼ばれるψで表される要素。
波動関数は、まさに量子が持つ未知の要素を示しています。波動関数は、量子の持つ波の性質を数式上にもたらすための要素です。それは粒子としての量子の不確実性とも言えます。実際に波動かどうかは知らないが、とにかくそれがあれば、かなり量子の効果を予測できるのです。
だがそれは本当に波なのだろうか?
現在主流とされている解釈は、その波とは、量子の存在確率の分布だというもの。ちょっと意味不明なのです。つまりある量子は、波の性質を発揮している時、その波の範囲のあらゆる場所に確率的に存在しています。それが波の性質が影を潜めた時に、確率的に存在していたどこかが定位置となる。(非常に重要なこととして、確率とか波動の収縮と呼ばれる、そのある定位置が定まる瞬間がいったい、いつ、どういった時なのか、普通、観察された時とされてはいるが、かなり曖昧な説明としか言いようがなのです)ということは、おそらく誰にもわかっていません。 そのタイミングも、いかにして収縮するのかも、量子力学の数式は示さないのです。( 「どこかで収縮するはず」というシステムは、実際我々が見るさまざまなものが確率の波動などではない事実を説明するために提案された完全推測にすぎないということになります)
もっとシンプルな解釈があります。それはつまり、確率的に存在してるのでなく、その全ての場所に存在している。その全てのいずれかが定位置のパラレルワールドが無数に存在しているのだという解釈等々。正直、こちらの方が理解はしやすい人も多いでしょう。パラレルワールドを怪しく感じる人もいるかもしれませんが、それは多分フィクションのテーマとして、それがよく扱われてきたが故の「パラレルワールド=フィクション的」という先入観のせいだと思います。
不確定性原理
確率の波動にせよ、パラレルワールドにしろ、量子の存在する位置が、その瞬間瞬間になるまで決まっていないのだとしたらどうか。それはある量子が、次の瞬間にどうなっているのか、確実な予測が出来ないという事を意味しています。
そんな事は当たり前だろうと思ったかもしれませんが、少なくとも「不確定性原理(Uncertainty principle)」と呼ばれるこの事実が示される以前の物理学者にとっては、それは当たり前などではありませんでした。今でさえ、誰もがこの不確定性原理なんてものを受け入れているわけではありません。
あなたは例えば、ボールを適当に投げた時に、それが最終的に、どこに落ち、止まるのかを、数センチ、数ミリ、もっと小さなレベルでの誤差もなしに、予測する事は出来ないかもしれない。しかしそれはあなたの無知と、能力の欠如のためにすぎないというのが、不確定性原理を信じない全ての者の意見なのです。
仮にあなたがボールの質量、より正確な形、というよりこの宇宙の全ての物質についての情報全てを知っていて、かつそれら全てを考慮に入れたシミュレーション構築能力を有しているなら、あなたは、ボールがどこに落ち着くのかを知れるはずです。不確定性原理なんてのが存在しないなら。
真空にすら揺らぎ
不確定性原理はそれ自体恐ろしいのですが、それだけではありません。真に恐ろしいのは、予測出来ない事ではない。そこに必ず何かがある事。
かつて、ある閉じた空間の中のどんな粒子も、エネルギーも一切取り去ってしまった時、そこは間違いなく真空になると信じられていた。物も力もない。あえて言うなら「空っぽという概念」だけがある、そんな空間。
だが、不確定性原理は、その真空とか、空っぽとかいうのを、ありえないものとして拒否します。
不確定性原理は、次の瞬間、そこにある量子の状態を予測出来ないと説きます。でも、もし真空なんてものがあるなら、量子は0という状態を簡単に予測出来てしまう。
我々が真空だと定義するような場にも、量子は現れる事がある。常にその可能性は存在している。量子の可能性か必ず広がっている、それはまるで揺らぎだ。この世界の中ならば、どこにでも生じている揺らぎ。実際に、それを「量子揺らぎ(Quantum fluctuations)」とか呼ぶ人はいるのです。
あまりにも小さく、大きな中心問題
物理学の「中心問題(Center problem)」ともされる対立の原因は、この量子揺らぎのせいなのです。
量子力学と一般相対性理論の対立。
量子揺らぎは真空の存在を許さないが、常識的なスケール(例えば1メートルとか、1センチとかの範囲)では、空間のあちこちに(例え極わずかではあっても)常に存在する量子の存在確率は打ち消しあい、我々からしたら真空といって問題ないような空間範囲も全然ありえます。
しかしスケールの小さな領域、つまりスケールの大きな領域にて打ち消し合う個々のひとつだけを切り取ったような領域においては、そうはいかず、量子揺らぎははっきりと現れるのです。
それは、もしも視覚的に表現するなら、上下左右、過去未来という時間すら入り組み、グチャグチャに混じり合う、少なくとも平らなどとは言えないような領域だと考えられています。実は問題とはそんなグチャグチャバラバラな領域なのです(こうしたスケール領域は、「量子的泡」と表現されることもあります)。
例えば、大した質量のない(一般相対性理論的に)平らな空間があるとします。その空間の一部を、具体的には1センチの1/1000000000くらいの範囲を拡大します。全体として平らなその空間の、その一部も当然平らです。さらにその1/1000000000の1/1000000000を拡大します。やはりそれは平らです。しかしその1センチの1/1000000000の1/1000000000のさらに1/1000000000の1/1000000の空間領域を拡大して見た時、我々は、だいたいの想定とは全く違うだろう世界を発見してしまうのかもしれません(これは一般相対性理論と量子力学の基本原理から実際に計算されてきた数値)。
ようするに、量子力学が示唆するグチャグチャな領域なのです。一般相対性理論的な考え方では平らなはずの領域です。しかし量子力学的な計算の上では、それほどにミクロな領域では、普通は小さすぎて無視できるような量子揺らぎ的なグチャグチャが目立つ。
こういったことは、かなり明らかに、ある事実を示しています。
つまり一般相対性理論か量子力学の、少なくともどちらかは間違っていて、0.000000000000000000000000000000001センチ以下とかの(いわゆる「プランク長さ」と呼ばれる)スケールでは、そのボロが出てしまうというわけです。
四つの力
十九世紀が残した混乱を解決しようとして生まれた様々なアイデアが、二十世紀の物理学に更なる混乱を生んでしまったのです。
特異点。宇宙誕生以前。存在確率の波動。どうあっても予測不可能な未来。理論上にすら存在出来ない真空。そして中心問題。
そして4つの力も。
原子以下のスケールが知られてから、そのスケール以下にしか影響を及ぼさない2つの力が明らかととなりました。2つの力とは、原子核を構成する陽子や中性子を結びつけている「強い核力(Strong interaction)」と呼ばれる力です。それと、粒子にある種の崩壊をもたらしたりする「弱い核力(weak interaction)」です。
もともと(十九世紀には)知られてはいた・電磁気力と・重力と、これら・非常に狭い範囲でのみ働く強いのと、・弱いのと、たった4つの力。この世界に、実は力と言えばその4つしかないとされています。でも4つの力は何が違うのか?この世界には、4つしか必要でないのか?あるいは4つも必要なのでしょうか?
量子場とメッセンジャー粒子
電磁気学では、電磁気が影響を及ぼす範囲を「電磁場(Electromagnetic field)」と呼びます。電磁気が発生した時、それは場を形成し、力はその場に及びます。電磁場は強い力、弱い力よりずっと以前からあった考え方だが、同じように強い力、弱い力も場を形成してるのかもしれないとは自然な発想だったのしょうか。
電磁場の最小要素を光子として、その最小要素が力というものを、場のあちこちに伝え合う。同じように強い力は「グルーオン(gluon)」、弱い力は「ウィークボソン(weak boson)」なる最小要素が、その場内にて、力を伝え合う。力はそうして伝わり合います。
それらは「素粒子(Elementary particle)」と呼ばれます、内部構造のない量子だとされていて、これらが力を持っていたり運ぶというわけではありません。
というより力とは何か?
光子、グルーオン、ウィークボソンは、その場内の物質を構成するような量子それぞれが、その時々に応じて、近づいたり、離れたりするような命令を伝えてわたるのだといいます。それが積み重なり、力という概念は生まれています。
そういう仕組みのために、光子、グルーオン、ウィークボソンは「メッセンジャー粒子(Messenger particles)」とも呼ばれます。
しかし本当にメッセンジャー粒子に内部構造はないのだろうか?
メッセンジャー、命令といっても、それが言葉通りの意味ではないのは確かです。言葉通りの意味である訳がありません。
グラビトン
4つの力だからひとつ残っている。重力のメッセンジャー粒子はあるのだろうか? あるとする人たちからもう「グラビトン(Graviton)」という名前まで与えられているが、理論上、計算上にすらそれを(他の要素と矛盾なく)定義するのは難しいとされています。
実は「超ヒモ理論(超弦理論)」が重要とされる理由の1つは、一般的にこの理論が、グラビトンが存在していることを前提としているからなのです。
超ヒモ理論は、素粒子の正体が、弦(ヒモ)と表現できるような( もちろん実際には、粒子の塊の物質である我々の領域の紐とは、違っているはずのものだが)最小要素なのです。
ヒモ、あるいは弦理論の発見
1960年代半ば。ガブリエレ・ヴィネチアーノ(Gabriele Veneziano)という物理学者が、強い核力について、ある発見をします。
紙の上のあらゆる幾何学を生んだ古代ギリシャ。
それに0の発見や、数字の簡単な表記方など、計算式の進化に多大な貢献をした古代インド。
それらの時代以降では、最も偉大な数学者のひとりレオンハルト・オイラー(Leonhard Euler。1707~1783)。
そのオイラーが発明した「ベータ関数(beta function)」と呼ばれる数式を用いれば、強い核力に関して、数学的に上手く記述出来そうだとヴィネチアーノは気づいたのです。
しかし確かに、ベータ関数は上手く働いたが、なぜこの数式が上手く働くのか、ヴィネチアーノにもわからなかったのです。
一次元のヒモという最初のアイデア
伝統的に物理学では、素粒子のような、内部構造のない最小構成要素を、点として扱ってきました。
しかし1970年に入り、南部陽一郎(1921~2015)、ホルガー・ニールセン(Holger Bech Nielsen)、レオナルド・サスキンド(Leonard Susskind)らがそれぞれ独立に、素粒子は、点でなく、一次元のヒモ(のようなもの)かもしれないと最初に唱えます。
彼らは、素粒子をヒモだと考えたなら、強い核力の記述に、ベータ関数が上手く使える事を示したのです。
しかしながら、この最初のヒモのモデルは、それから成された予測が、精度のより向上した素粒子の実験結果といくつも矛盾したために、間違いだったとしてすぐ廃棄処分となりました。
美しいが正義
ヒモ理論は矛盾が見つかり捨てられたが、忘れ去られはしませんでした。その数学的構造の美しさのために、この理論の深淵には何かが必ずあると、一部の者は感じていたのです。
ヒモ理論は強い核力のメッセンジャー粒子、グルーオンについて「ヒモの振動パターン」というアイデアにより、上手く記述しましたが、しかしまた強い核力とは関係なさそうなメッセンジャー粒子(らしい何か)、あるいはヒモの全く未知の振動パターンを前提として含んでしまっていたです。
1974年、ジョン・シュワルツ(John Henry Schwarz)とジョエル・シェルク(Joël Scherk)は、その未知の振動パターンの、(メッセンジャー粒子としての)特性が、重力のメッセンジャー粒子として仮定されていたグラビトンの(予測されていた)それらと一致する事に気づきました。
シュワルツとシェルクはこの(例え間違いであったとしても、それでも間違いなく)素晴らしい発見を武器として、ヒモ理論が捨てられていたゴミ箱を破壊したのです。
2人はこう主張しました。「ヒモ理論が間違いだと思われたのは、それが単に強い核力のみを対象とするものだと勘違いされていたせいだ」と。それはつまり、ヒモ理論は、グルーオンだけでなく、グラビトンをも包括する素粒子理論だという主張でした。しかしこの時はまだ、この復活したばかりの議論は注目されませんでした。
統一理論か?
だが物理学界に無視されながら、シュワルツは諦めなかったのです。彼は信念を持って研究を続け、1984年、マイケル・グリーン(Michael Boris Green)とともに、ヒモ理論の状況をついに変えます。その頃、ヒモ理論には、量子力学との矛盾も見つかっており、もう完全に破綻しているというのが多くの者の見解だったが、シュワルツとグリーンは、その量子力学とヒモ理論の矛盾を取り除くのに成功したのです。
さらに彼らに修正されたヒモ理論は、強い核力と、重力だけではありません。今度はこの世界に存在する四つの力全てを含む壮大なものと化していたのです。
つまり、それはそのままヒモ理論が、真の統一理論である可能性を示していました。
第一次ヒモ革命
シュワルツとグリーンの成功と、示されたヒモ理論の可能性に触発され、多くの物理学者が、自分のノートに、(もはや単なる応用数学とは思えないほどに)複雑で難解なヒモ理論の数式を書きました。
1984年から1986年、『第一次ヒモ理論革命(First string theory revolution)』と呼ばれるこの3年間、世界中の優れた物理学者たちが、ヒモ理論を研究、発展させ、この宇宙で知られる数多くの物理特性のいくつもが、ヒモ理論から自然と導き出されると証明されていきました。ただしこの一度目の革命の熱はすぐに冷め、あっさりと終局していく。原因は明らかに、ヒモ理論を構築する難解すぎる数式の山なのです。
物理学の研究では、難解な数式に直面することなどよくあるようなイメージだが、ヒモ理論の場合は、必要な数式を特定する事すら難しかったのです。それでも物理学者たちは苦労の末にヒモ理論を記述するための数式、でなくその近似をなんとか見つけ、近似的にでもそれを上手に使ったのです。
だが近似的にでも、ヒモ理論に関して様々な事を明らかにしながら、まだ多くの問題も残っていて、ついに物理学者たちは行き詰まります。近似的に記述出来る限界に到達してしまったのです。
その素晴らしい財宝の島を確認しながら、彼らの船はそれ以上進めなくなってしまったのです。こうしてヒモ理論、最初の革命は幕を閉じました。
素粒子は全てヒモ
ヒモ理論以前のように、素粒子を点として考える場合の重大な問題のひとつは、素粒子に複数の種類があり、かつその特性の違いについて、ろくな説明が出来ないという事です。例えば同じく素粒子とされる電子と「クウォーク(quark)」(陽子とか中性子を構築する素粒子)では質量が違っています。相対性理論によると、質量とはエネルギーなので、つまり最も基本的なモノであるはずの素粒子は、種類によって別々のエネルギー量を抱えている。内部構造がない素粒子に種類ごとのエネルギーとは奇妙です。しかしヒモ理論ならば、素粒子を(我々が種類分けしてるどんな素粒子も)一次元の小さなヒモとして扱い、素粒子の抱えるエネルギーをヒモの振動パターンとして解釈します。そうする事で素粒子に種類がある(ヒモの振動パターンの違いという)理由を提示できます。つまり弦楽器がその弦の振動パターンによって音を変えるようなものなのです。ただし忘れてならないのは、エネルギーは最小単位を持つ不連続(デジタル)的なものだという事。つまりヒモの振動パターンも不連続のはずです。
もうひとつ気にした方がいいかもしれない。
それは、必ずしも振動パターンは無限でない事を意味してはいないということ。当たり前ですが、エネルギーが「ある数の整数倍の数」しかありえないのだとしても、「ある数の整数倍という数」は無限ですから。また、電子などのように、素粒子だと考えられながら、明らかに特性(役割)の異なっているメッセンジャー粒子についても、ヒモ理論は、電子などとの本質的な違いは、振動パターンの違いに過ぎないと説きます。
ヒモ理論が正しいとするなら、ヒモのありうる振動パターンが生じさせうる特性が、観測(あるいは計算)される素粒子の特性と一致するはずでです。しかしこれに関してはまだ上手くいってるとは言えないようです。だが異なる素粒子の違いについて、ヒモ理論が説明出来る可能性がそれで消える訳ではなく、これは明らかに点粒子モデルよりも優っている要素なのです。
かなり強い張力、小さな長さ
1974年にシュワルツとシェルクが、ヒモ理論はグラビトンを含むものかもしれないと示した時、二人は計算式より、そのグラビトンと思わしき振動パターンが伝える重力の強さが、ヒモの張力(ヒモがどれほど強く張られているか)に反比例する事を見いだしました。
これは重力の強さから、ヒモの張力を予測出来ることを意味し、実際二人はヒモの張力を予測しました。
張力というのはしばしば重さの単位で示されるが、参考までにギターの弦の張力が平均して50グラムくらいです。ヒモはというと、シュワルツとシェルクが予測したヒモの張力は1000000000000000000000000000000000000000000000グラムであった。これは「プランク張力(Planck tension)」と呼ばれる張力の強さで、この張力からさらにヒモの長さを計算できるといいます。そして典型的なヒモの長さは「プランク長さ(Planck length)」と呼ばれている、0.000000000000000000000000000000001センチくらいだという事も示されました。
ヒモの張力の莫大な強さは、ヒモを少し揺らすのにも莫大なエネルギーを要する事を意味しています。そして、それはそのままヒモの少しの振動、例えば「ある数の整数倍」の「ある数」すら莫大なエネルギーを生む事をも意味しています。
グラビトンの場合
莫大なエネルギーといってもそれは素粒子のスケールでという話です。例えばヒモが生み出す、プランクエネルギーと呼ばれる最小のエネルギーは、質量で表すと「一粒の塵」ほどであるといいます。でもこれは明らかにおかしい。一粒の塵は、我々から見たらわずかな質量にすぎないが、それでも電子とかクウォークとかより明らかに大きな質量である。5を整数倍していって、どこかで2や3が現れるなんてあるはずがないでしょう。
そこで量子力学の不確定性要素の出番となります。不確定性要素は、最小要素のヒモにまで不確定性をもたらします。つまり常に完全に静止しているヒモなどありえない。ヒモのスケールでは、量子揺らぎは激しく、その揺らぎは、ヒモの実際の振動パターンと打ち消しあう事がある。こうして、我々に知られた電子やクウォークの質量が生まれてくる。ところで、(それは明らかにいかなる重力下でも不変の速度で伝わるために)グラビトンの質量は0かもしれないと予想されていますが、ヒモの振動パターンと量子揺らぎが完全に打ち消しあう可能性もあると、シュワルツとシェルクは示していました。つまりヒモ理論では、質量0の振動パターン、グラビトンも全然ありえるという事です。
中心問題の解決
ヒモ理論の最も魅力的なところのひとつは、中心問題を解決している事なのは間違ありません。中心問題はあるスケール以下では、量子力学的な量子揺らぎと、一般相対性理論的な歪みがない場合の穏やかな空間を合わせて考える事が出来ないというものです。しかし最小構成要素すら、空間的な広がりを持ったヒモだとするなら、そしてそのヒモの最小スケールが、中心問題で舞台になるスケールよりも大きいとすれば、問題は消え去る。というか中心問題など、最初からなかったという事になります。
しかしヒモかどうかはともかく、最小構成要素にすらいくらかのスケールを持たせるなんて単純なアイデアが、ヒモ理論以前にはなかったのかというと、普通にあったのです。
最小構成要素にも大きさのスケールがあるという可能性は、ヒモ理論以前にも、幾度も考えられてきたが、しかし上手くいきませんでした。最小構成要素、つまり素粒子にある大きさを持たせてしまうと、たいていの物理的要素が壊れてしまうのです。ヒモならば上手くいくから(あるいはいきそうだから)この理論は革命的だと言われたわけです。
スピン
1925年、ジョルジ・ユーレンベック(George Eugene Uhlenbeck。1900~1988)と、サミュエル・ハウトスミット(Samuel Abraham Goudsmit。1902~1978)が、明らかとなっていた電子の磁気的性質を、電子が回転運動を行っていると考えれば、上手く説明出来ると示し、この回転運動は「スピン」と呼ばれるようになりました。点だと考えられていた素粒子である電子が回転運動など意味不明だが、スピンの性質は、やがて、素粒子(とされるもの)全てに備わっているらしい事が明らかにされます。量子力学的尺度によるスピン速度を数値として表す事もされています。それによると、電子など、「フェルミ粒子(Fermion)」と呼ばれる、物質を構成する量子のスピンは1/2。「ボース粒子(Boson)」と呼ばれる、グラビトン以外のメッセンジャー粒子のスピンが1。そしてグラビトンは(存在するとしたら)スピン2だと計算により示されています。もちろんスピンと呼ばれていても、それはコインを回転させたりする回転運動とは全然違うものです。
素粒子のスピンは、不変の性質のようなもので、スピンしているのとスピンしてない素粒子があるとかではなく、素粒子が存在するという事は、それは必ず固有のスピンを持っているというようなものなのです。
超対称性
この世界には「対称性(symmetry)」があるとされています。「右から見ても左から見ても同じである」という事でなく、ある物理法則は、宇宙のどの場所でも等しく働くというもので、「物理学的な対称性」などと呼ばれています。例えば重力の法則は宇宙のどこでも働くから、我々は行った事のない火星などで、人間がどれくらいジャンプできるのかを予想したりできます。この自然で何より決定的な対称性とは、観測される互いの運動です。誰もが自分の視点を持ち、ある物が回転している時、他のどんな止まっている者にも、それは回転している。通常の回転とは違う、しかし回転運動ではある素粒子のスピンに対応するような対称性があるだろうか? あるとして、そんな対称性を物理学者は、「超対称性(supersymmetry)」と名付けました。ヒモ理論は元々、フェルミ粒子の振動パターンを上手く示せずにいたのだが、超対称性を組み込む事で、その問題は回避できました。
そういう感じで、着実にその物理学界におけるその立場を強めていったヒモ理論ですが、まだまだ道は険しかったのです。
カルツァ・クライン理論
アインシュタインが相対性理論により、時空間の性質を暴きだしたのと同じくらいの頃、テオドール・カルツァ(Theodor Franz Eduard Kaluza。1885~1954)という人が、この世界の空間次元は、実は三次元でないのかもしれないと主張しました。これはとんでもない事のように思えるかもしれないが、実はそれほどでもなかったりします。
例えば1本の棒を想像しよう。棒の表面は明らかに二次元である。棒の表面に乗る虫の位置を説明するためには、棒の上下左右の位置情報がいる。
しかし棒を遠く、その横幅が全くわからないほど遠くから見たらどうか? 棒には上下しかないように、つまり一次元に見えるであろう。本当は二次元であるのに。
同じことは三次元に思えるこの空間全体にも言えます。
例えばこの空間が実は四次元だとして、四つ目の次元が十分小さく、折りたたまれていたなら、それを我々の認識できるスケールでは確認出来ないという事はありえるとカルツァは述べました。
カルツァのアイデアは後に、オスカー・クライン(Oskar Klein。1894~1977)という人がより具体的な形で示した事で有名になり、今ではそのような、小さすぎて確認されていない次元があるという考え方は、「カルツァ・クライン理論(Kaluza-Klein theory)」と呼ばれています。
実は四次元であるならば
カルツァは空間が四次元だとしても、適切な修正を行えば一般相対性理論が成り立つ事も示し、アインシュタインもそれを認めました。それにアインシュタインはカルツァの論文を素晴らしいと褒め称えたのです。それは実は、空間は四次元であるというカルツァのアイデアが、重力と電磁気力を繋ぐ鍵であるかもしれなかったからです。
人の目には一次元にしか見えない棒の表面でも、実は二次元であるならば、より小さな虫にとってはしっかり二次元であろう。同じように我々には感じとれない小さな次元でも、その次元と同程度か、より小さなものにとっては、それはちゃんと次元なのである。
カルツァは、重力が四次元空間にて働く場合の相対性理論の式を実際に書いてみたが、その形はなんと電磁気力のそれと似ていたのです。重力と電磁気力には何か関わりがあるのかもしれない。もっとはっきり言ってしまえば、実は四次元のこの世界にて、力といえば1つであり、4つ目の次元に影響を受けた力が電磁気力、受けなかった力が重力なのかもしれない。しかしそうだと考え、実際の世界に、その考えを適用しようとしても上手くはいかなかったのです。
実は10次元
カルツァは失敗しましたが、彼以降、強い核力と弱い核力が知られると、高次元モデルが上手くいかなかったのは、単にデータ不足だっただけなのかもしれないとも考えられるようになりました。でも電磁気力、重力に加え、強い核力、弱い核力まで同じ力として扱うためには、カルツァが前提としたような四次元空間ではまだ足りない。五次元、六次元とさらに空間次元の数を増やす必要があるのは明らかでした。
ここでヒモ理論は奇妙な変化を遂げます。
ヒモ理論は、中心問題を回避するほどには、よくあるヒモを大きく仮定しているものの、それでもプランク長さという大きさは量子力学的な効果を無視できるようなスケールでは決してない、そのスケールに関係する量子力学的計算の中には「マイナスの確率」など不安要素がいくつもありました。これはまた量子力学とヒモ理論の対立だったです。しかしそれも物理学者たちは上手く解決します。問題が残ったとすれば、その解決策がカルツァ・クライン理論だった事です。二次元のヒモと三次元のヒモでは、その振動に使える次元が異なっている。縦横上下にしか振動出来ない二次元と違って、三次元では奥手前にも振動できる。このように振動に使える次元を増やしていき、ついにその空間が九次元に達した時、その空間内でのヒモの振動パターンは、量子力学的計算からでる無意味な(と思われる)答を回避できたのでした。
つまりヒモ理論は、高らかにこう述べていたのだ。
この世界は(時間を合わせて)実は10次元である
隠された次元の幾何学的形体

ヒモが小さく、小さな隠された6次元を含んだ9次元を振動するものなら、ヒモ理論を形成する上で、必要なヒモの振動パターンが全て可能な6次元の形を求めるという方法で、隠された6次元の幾何学的な形を探る事が出来る。実際にそうして、隠された6次元の形は数万程度に絞られ、それらの形は「カラビヤウ図形(Calabi–Yau figure)」と名付けられました。数万といえば、まだまだだと思うかもしれないが、幾何学的形体なんてのは、それこそ無限にあるのだから、これは凄い進歩なのです。仮にいつか、隠された6次元空間が見つかり、その形が、カラビヤウ図形のどれかなら、ヒモ理論のかなり強力な証拠になるくらいにはなるでしょう。
五つある
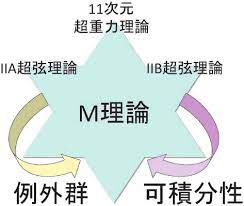
ヒモ理論には、数学的、とか幾何学的とかそういうの関係なく、統一理論としてもっと致命的な問題もありあました。研究が進むにつれ、ヒモ理論には、導き出される物理はどれも同じなのに、その機構の細部が違う五つのタイプがある事が明らかとなってきたのです。
五つのタイプは、それぞれ名前をつけられています。すなわち、
『I型(type I)』。
『ⅡA型(typeⅡA)』。
『ⅡB型(typeⅡB)』。
『ヘテロO(32)型』あるいは単に『ヘテロO型』。
『ヘテロE-8×E-8』あるいは単に『ヘテロE型』。
以上の5つ。
これはいったいどういう事か? ヒモ理論は統一理論ではなかったのか? 普通、物理学者が統一理論という言葉を使う時、それは、唯一何の矛盾もなく、この宇宙全てを記述する唯一無二の理論を指しています。それが5つも?
ヒモ結合定数
その五つもあるヒモ理論自体をひとつに統一する試みこそが、1995年から始まったとされる『第二次ヒモ理論革命(Second string theory revolution)』でした。
実をいうと僕もこの頃から本格的に超弦理論の勉強を仕事の傍らで少し勉強をし始めています。
ヒモが量子揺らぎの影響により二つに別れたりする事があり、それがどれくらい起きやすいかを表す「ヒモ結合定数(String coupling constant)」という数がある。このヒモ結合定数は、ヒモの振動パターンにもかなり関係する数のために、理論全体においても重要な数です。ヒモ結合定数(以下、単に「結合定数」)は、五つのヒモ理論いずれにもあり、そのどれも結合定数が1以上になると、途端にわかる事が少なくなるため、基本的にヒモ理論研究者は、結合定数1以下の場合を想定し、研究を進めてきました。
しかし1995年、エドワード・ウィッテン(Edward Witten)は高らかに述べた。鍵は結合定数1以上の場合だと。
I型理論の結合定数を1以上に増大させる。するとどうか?
I型理論に関してわかる事は極端に少なくなる。しかしわずかにわかる要素は、なんと結合定数1以下の場合のヘテロO理論のそれと一致していたのです。
すなわちI型理論は、ヘテロO型理論と裏表一体、「双対性(Duality)」と呼ばれる関係にあったわけです。
さらに驚くべきは、ⅡB型理論の結合定数を大きくしていくと、なんとかすかにわかる要素が、自身、つまりⅡB型理論の結合定数の低い場合と一致したことです。
I型とヘテロO型
ヒモ理論も、大きなスケール、低エネルギーの状態を考える場合は、伝統的な点粒子の考え方で近似的に記述できます。カルツァ・クライン理論は、普通に点粒子的なモデルにも影響を与えていたので、点粒子モデルにも多次元のものがあるが、ヒモ理論は10次元か、あるいは11次元時空の点粒子モデルが近似としてよく使えました。
もちろん超対称性を点粒子モデルに組み込む事も出来るが、その組み込み方によって、10次元点粒子モデルは、4つの別タイプを作れます。
その4タイプの内、3つはⅡA型ヒモ理論、ⅡB型ヒモ理論、ヘテロE型ヒモ理論の近似として有効でしたが、4つ目はⅠ型とヘテロO型のどちらの近似としてもよく使えるように思われました。
やはりI型とヘテロO型には何かがあるのだろうか?
11次元へ!
ⅡA型やヘテロE型の結合定数を大きくした時に見えてきたものこそが、おそらく答でした。その時、現れたのは引き伸ばされ、「ヒモでなくなったヒモ」だった。理論の上で、ヘテロE型の結合定数を大きくすると、ヒモは引き伸ばされ、一次元でなく、二次元の膜に変化したのである。それは予想外に現れた11番目の次元でした。
これはある事を示しているように思えました。
すなわち、そもそも10次元宇宙のヒモ理論モデル自体が、実は結合定数が低い場合の(ヒモが一次元に見える場合の)真なる11次元モデルの近似でしかなかったのかもしれないのです。この宇宙は4次元でも10次元でもなく11次元だったのでした。11次元目はヒモ自体に隠されていたわけです。
大統一
やがてⅠ型とヘテロO型の間にあるような双対性は、結合定数でなく、ヒモそのものの幾何学的パラメーターを変更するという手順により、ⅡA型とⅡB型の間、ヘテロO型とヘテロE型の間にも示され、五つの理論の繋がりは徐々に強化されました。さらに注目すべき事は、ⅡA型やヘテロE型の結合定数を上昇させる事で姿を見せる11番目の次元という要素が、その後に他の型の理論へと変化させても残るという事です。
それは何を意味しているのでしょうか?
5つあると思われていたのは、実は深淵にてひとつとなり、そこでは、さらにもうひとつの次元が存在していました。
こうして本当の意味での、唯一無二の統一理論。すなわち、たったひとつしかない11次元宇宙のヒモ理論、M理論(Theory of M)」がついに物理学界に転がり出てきたのです。
ヒモについて
ヒモ理論のヒモ素粒子は、1つ1つは、小さな振動するひもの輪あるいはループでできていると考えられている。そして典型的なひもの輪の長さはプランク長さほど。ヒモ素粒子は、(我々から見るとそれでも十分に小さい)原子よりかなり小さい(原子核の10^20分の1ほど)。ヒモがヒモであることを実際に確認するのが困難であることも当然と言えます。
パターン無限?
我々が基本的な素粒子と認識してきたものの、力荷とか質量といった性質は、超ヒモ理論的には、ヒモ素粒子の振動パターンの影響です。
ヒモの振動パターンは無限だろうか?
可能性は高いと思われています。ヒモに、例え1(でなくともある数)の整数倍の振動パターンしかないのだとしても、普通に考えればそれの揺らし方を強くし続ける事は出来る。例えば楽器の弦ならば、それが実は原子が結びついた物であるために、原子同士の結びつきを破壊するほどの勢いで扱ってしまうと、千切れたりします。だが素粒子のヒモは内部構造がないので、そもそも千切れるという事はありえません。しかし、ある数の整数倍の振動パターンしかないとはこのようにも考えられる。つまり、振動パターンをヒモの波と山、つまり波長の量として考えると、最小の波長いくつか、つまりヒモ全てを占めているパターンが、ヒモの奏でられる最高エネルギーだということです。しかし最小構成要素のヒモに整数倍振動パターンとその限界?ヒモ理論が正しいとして、また新たな疑問がどうしても浮かんでしまいます。ヒモに内部構造は本当にないのでしょうか?
いったい、どのように振動パターンが性質として現れるか
ところで、ヒモ素粒子の振動パターンが、質量などの原因なのだとして、具体的にはどのように、振動が他の性質として現れる(理解される)のか。実は質量の場合は、むしろわかりやすいとされいます。特殊相対性理論は質量とエネルギーが等価的であることを示しています。つまり、ある物質のエネルギーが大きいなら、大きいほど質量も大きい。そしてある振動パターンのヒモ素粒子のエネルギーは、その振幅(山あるいは谷の最大変位)と波長に(ようするに揺れの強さに)関連する。振幅が大きいほど、あるいは波長が短いほどエネルギーは大きい。そのことは直感的にもわかりやすいでしょう。振幅の大きさ(大きな変化幅)と波長の短さ(早い周期)は、明らかに激しい振動パターンを示し、もちろん何らかの動きは激しい方がエネルギーが大きいと考えやすいですね。そしてそれはつまり質量の大きいことも意味します。したがってヒモの振動パターンの激しさは、素粒子の質量を決める訳である。重い粒子は、大きなエネルギーで振動するヒモで、軽い粒子は、小さなエネルギーで振動するヒモとなります。
ある物質が発生させる(それが時空の歪みであれ、何であれ)重力を、その物質の性質と考えることはできるだろう。その場合、つまり重力という性質も、物質の質量が決めているはず。そしてヒモの振動パターンが質量を決めるから、そのパターンは重力とも関連します。同じように、ヒモの振動パターンは、重力以外の力、つまりヒモ素粒子が有する電荷、弱い力荷、強い力荷を決定します。メッセンジャー粒子についても同じ。光子、グルーオン、ウィークボソンといったものは、ヒモの振動の、別の『共振(共鳴。resonance)』、すなわち他物質(ヒモ)の振動パターンをさらに誘発するパターン。そして特に、ヒモ理論が注目を集めた重要な理由は、ヒモの振動パターンの中に、グラビトン(すなわち重力のメッセンジャー粒子)の特性と一致するものがあるようだったこと。そのことは、ヒモ理論において、重力というのが理論から導出される必然的な要素であるということを示唆しています。
低いエネルギースケールの世界
先に述べたように、シェルクとシュワーツはグラビトンのヒモ振動パターンの発生させる力は、ヒモの張力に反比例することを見いだし、そこからヒモの莫大な張力(プランク張力)をも示しました。それはさらにヒモに関するいくつかの情報を示します。
素粒子ヒモは、楽器の弦のように両端をとめて長さを調整されていません。しかしヒモは、そもそもその莫大な張力から、微小なサイズに縮まっているループと考えやすい。典型的なヒモの長さはプランク長さとなります。また、素粒子ヒモの振動するループの典型的エネルギーは非常に大きいのです。まずそれを振動させるのに必要なエネルギーが、(その強い張力のため)非常に大きいはずという直感がおそらくそのまま適用できます。ヒモが振動しているなら、そこにある(ヒモが有している)エネルギーは非常に大きいはずです。
さらに量子力学が正しければ、エネルギーは不連続(デジタル)的なもので、ヒモの振動パターンも、そのデジタルに縛られ、つまり典型パターン(プランク・スケール)を決め、ます。その典型パターンは通常なら、例えば陽子などの質量(エネルギー)より大きい訳ですが、やはり量子力学の不確定性原理が示唆せる、量子的じたばた(それはヒモのスケールにおいて、マイナスのエネルギー)が、ヒモの典型的振動パターンのエネルギーの大部分を打ち消します。つまりミクロ領域の打ち消しあいのために、単体のヒモの最低エネルギーパターンよりも、振動パターンのエネルギーは結局かなり低くなり、物質やメッセンジャー粒子の質量(エネルギー)の付近になると考えられるのです。そしてシェルクとシュワーツが見いだしたグラビトンの候補の振動パターンは、エネルギーの打ち消しが完全なものでした。これはグラビトンの質量がゼロであることを示唆していますが、そのことは少なくとも普通の推測と一致します。重力は、一般相対性理論によれば、やはり質量ゼロとされる光と同じ速度で伝わるため、グラビトンも普通に考えるなら質量ゼロのはずです。ただ、そもそも振動パターンは無限に考えられる(それを制限してそうな要素は、「ある数の整数倍」というものしかないが、ある数の整数倍は無限)。量子的じたばたなどほとんど無意味なくらいに大きなエネルギーの振動パターンがいくらでもあるはずです。ではなぜ、我々が現在発見できているよりも、さらに多くの、もっと大きな質量の素粒子が全然見つからないのでしょうか。
ビッグバンの時には、そのような非常に重い粒子を生むほど強力なエネルギーが発生していたと思われていますが、しかしそれが現在までに、残っているにしてもどのくらい残ってるものでしょうか。
我々は、つまり、低いエネルギースケールの世界に生きているのかもしれない。
何が混乱した考え方なのか
素粒子ヒモという最小のスケールは、一般相対性理論と量子力学が矛盾するスケールという概念を消してしいます。本当にそうなのでしょうか。我々は「神の視点」など持っていません。そもそも自分たちが物体構造である我々が、何か物体の構造について知る方法は、間接的なものに限られています。我々は、物体にぶつかった作用の方向がどう変わるかを観察することで、 その舞台の様々の情報を定義できる。例えば我々が「何かを見る」と言っている時、実際に起きていることは、物体に反射された光子を取得し、それから得られた情報を脳が理解するからです。粒子加速器も、電子とか光子をぶつからせ、飛び散るものを検出器に捉えさせることで、物体構造を調べます。しかし、ぶつける粒子(探査粒子)より小さいものを感知するのは困難なのです。探査粒子が探査対象粒子より、大きければ大きいほど、 ある反応をもたらした行動パターンの数は多くなりすぎるからです。例えば、地球上でリンゴを地面にぶつけたとして、そこに見られる反発から、地球が球体なのか、平らな大地なのか、あるいは球にせよ、平らにせよ、それがどのくらいなのかということをどうやって見極めろというのかということになってしまいます。粒子加速器では、陽子や電子が探査粒子として使われてきたが、これらのスケールでは、すでに量子論の影響がかなり現れていまする。量子的波長が、探査粒子の位置の不確かさの幅を決め、その幅も探査の尺度となります。探査粒子が(従来の理論でお馴染みな)点なら、探査誤差の範囲は、探査粒子の量子的波長にほぼ等しいと思われます。ようするに点粒子の探査感度に関して、量子じたばたが邪魔になるのです。しかしある粒子の量子的波長は、その運動量、大雑把に言ってエネルギーに反比例します。したがって点粒子のエネルギーが増したら、その量子的波長は短くなる。エネルギーを高めて、高めて、高めれば、理論的にはどこまでもミクロな構造を探れるだろう。でも、すでにその最も基本的な状態から、二次元の幅を持っていると考えられる素粒子ヒモの場合、その大きさより小さいものの構造(つまりプランク長さより短いスケールで生じる構造)を探ることができなません。1988年頃、デイビッド・グロス(David J Gross)とボール・メンデ(Paul F Mende)は、量子力学を合わせて考えると、ヒモのエネルギーを高めつづけても、細かい構造を探る能力がどこまでも高まるわけではないことを示しました。プランク長さのスケールで構造を探るのに必要な値以上にエネルギーが増したなら、後はエネルギーをどれだけ大きくしようと、探査精度は高まらない。ヒモは大きくなり、短距離スケールでの感度はむしろ低下してしまう。理論的には、(凄まじいエネルギーを注ぎ込んだ場合)、 我々が普通に見ることができる大きさのヒモもありえます。それとヒモという最小スケールが正しいなら、ようするに、 一般相対性理論と量子力学が矛盾してしまうと思われるのは、ありもしない(ヒモ以下の)スケールを、我々が勝手に想定してしまったために生じた矛盾と言えるでしょう。本来1から10の整数しか使えない計算プログラムがあるとして、0.1や0.2が使えるということを想定して、計算結果がおかしくなってしまっているようなものです。この宇宙は全てを、0.2も0.01もあるはずだと考えるのもいいが、そうではなかったのかもしれないのです。
超対称性はなぜ必要か
スーパーパートナー
量子力学的なスピンというのは、点粒子にも定義される性質です。言わば古典的宇宙には存在しなかった、つまり19世紀までに生きていた誰1人として、想定もしていなかった、我々が知らなかった類いの回転運動でなのです。そして、普通の回転運動について成り立つとされる、(物理学的な空間の中では、あらゆる方向は対等に扱われる)回転不変性のような対称性原理が、スピンにもありうるか。そういう疑問から、複雑な数学的分析により、自然法則の新たな対称性、超対称性は発見されました。
1970年代頃。もし宇宙が超対称的なら、自然の粒子はスピンが半単位 (1/2)だけ異なる対をなすものという示唆があった。そうした粒子対は(それが点か、振動するヒモループかにも関係なく)「スーパーパートナー」と呼ばれます。そしてこの発見と、物質粒子がスピン1/2、メッセンジャー粒子の一部がスピン1を備えているという計算結果は、興味深い流れになっていきました。でも、超対称性があるとして、それを組み込んだ標準モデル(従来の点素粒子を利用し、かつ重力は取り入れていない統一理論。普通はヒモ理論のものほど奇妙な世界観ではないとされるが、(ヒモの振動パターンでそういうものが決まる)ヒモ理論と比べると、素粒子の力荷や質量などの数値がどのように決まっているかを説明するのが困難とされています。もちろん重力を上手く組み込むことにも成功していない)の中で、発見されているどの粒子も、互いのスーパーパートナーではないことは1970年代半ばには示されていました。もっと重要なことは、どの粒子の未発見のスーパーパートナーも、スピンが半単位小さいもののようだったことです(例えば電子やニュートリノとクォークにはスピン0のパートナーがあるということになります)。
標準の大統一理論において
おそらく超対称性は、他の対称性と比べて、特別何か、神秘的なものというようなものではありません。自然が、いくつかの数学的な対称性の中で、超対称性だけをシステムに組み込んでいないというのは、直感的には奇妙な感じですね。さらに超対称性は、例えば標準モデルにおける(超対称性がないとすれば発生する) 非常に細かな数値調整を必要とする(つまり特定の数値に強く依存する)量子的過程に関連する破壊的問題の解決を簡単にします。超対称性が正しいなら、 スーパーパートナーである、スピン整数粒子(ボソン)と、スピン半整数粒子(フェルミオン)は対で生じ、量子力学的な破壊性の原因である量子効果を、やはりいくらか打ち消しあう傾向を見せるはずなのです。1960年代に、グラショウ(Sheldon Lee Glashow)、サラム(Abdus Salam。1926~1996年)、ワインバーグ(Steven Weinberg。1933~2021)は、電磁力と弱い力の関連を証明しました。その後この研究の発展は、さらに強い力をも取り込んだ、3つの力の「大統一理論(grand unified theory。GUT)」へと続いていきました。これは1974年に、グラショウとジョージャイ(Howard Georgi)により最初に提唱されたものです。電磁力と弱い力を統一する「ワインバーグ=サラム理論(Weinberg-Salam theory)」では、宇宙の温度が絶対温度で10^15Kくらいになった時に、それまで統一的だった力が電磁力と弱い力に分かれる。グラショウとジョージャイは、強い力が統一的力から分離するのは、絶対温度でおよそ10^28Kくらいであるはずと示しました。
力はいつ同じになるか
物理学的な場には量子的ゆらぎがあります。例えば電子の場を調べるなら、実際には電子の場全体で起きている瞬間的な粒子-反粒子の出現と消滅の嵐を通していると言えます。そして、そのミクロのゆらぎの嵐のせいで、電子の力の強さは見極めにくくなる。しかし電子に近づけば、間にある粒子-反粒子の量は少なくなるはずだから、量子揺らぎの影響も弱まる。結果的に、電子に近づくにつれて電子の場の強さは増すことになります。この場の強さの高まりは、量子力学的現象で、距離が短いほど電磁力の引力(あるいは斥力)が強まるというような古典物理現象とは違う。量子効果は、スケールを短くするほどに、電磁力の場の強さ自体を増します。さらに1973年、 グロス(David Jonathan Gross)とウィルチェック(Frank Anthony Wilczek)、それにポリツァー(Hugh David Politzer)が、電磁力以外の場の、量子効果の影響の研究で、粒子の出現と消滅の量子効果が、強い力と弱い力の強さを増幅させることを示しました。つまり、これらの力は短い距離スケールほど、固有の強さを弱めます(電磁場と逆)。そしてジョージャイとワインバーグ、それにクイン(Helen Rhoda Arnold Quinn)は、3つの力の強さは本来すべて同じだが、それは我々に観測可能なスケールにおける、量子的作用の影響の違いのせいで、 異なっているように見える、という世界観を提唱。10^-29センチメートル(プランク長さの一万倍程度)ほどの距離スケールでこれらの力を調べたなら、その強さは等しいように見えるはずであると。 しかしその後の研究で、ジョージャイらのモデルにおいては、3つの力は小さな距離スケール(高エネルギー下で)ほとんど一致するものの、完全には一致しないことも示唆される。しかしこの不一致は、理論に超対称性を組み込んだ場合の、スーパーパートナー粒子がさらにもたらす量子的ゆらぎの影響を考慮すると、その強さをちょうどよく収束させられるのです。
そして力の強さの収束につながる計算が示唆する、スーパーパートナー粒子の(知られる粒子と比べた場合の)重さは、他の研究結果とも矛盾しないと考えられました。スーパーパートナー粒子の大きな質量は、それを一瞬でも造るための莫大なエネルギー量も意味していて、それがなぜ、エネルギー加速器でもなかなか発見できないかを説明できるのです。
ヒモ理論研究所による修正
超対称性は、ヒモ理論モデルでは、その必然性に関してさらに説得力が増します。
1960年代末頃にヴェネチアーノの研究から出たヒモ理論には、当時はまだ発見されていなかった超対称性は組み込まれていませんでした。その初期ヒモ理論は、ヒモの振動パターンのスピンが全て整数であることを示していて、フェルミオン・パターンを組み込むことが困難だったのです(だからボソンヒモ理論と呼ばれる)。そしてボソンヒモ理論には、質量がマイナスである振動パターンが1つあるようだった。どうもそれは、いわゆるタキオン(超光速粒子)らしい。フェルミオンをボソンひも理論に組み込む形で修正しようという研究が進むと、どうも理論のボソンの振動パターンとフェルミオンの振動パターンは対をなすかもしれない可能性が出てきた。そして超対称性が組み込まれた新しいヒモ理論(超ヒモ理論)が生まれた。ボソンヒモ理論で問題となっていたタキオンの振動は、超ヒモ理論では問題にならないことが証明されたのは、特に重要なことでしょう。そして、ヒモ理論からとった超対称性は、点粒子理論にも活用できたことから、結果的には、超対称的量子場理論とか、超対称的標準モデルといったものの研究もかなり進みました。M理論で合わせられると考えられる超ヒモ理論の5つのタイプは、超対称性の、理論への組み込み方に関連しています。
11次元宇宙はどう動作するか
超ヒモ理論には、我々に馴染みがあまりない、隠されてるかのような6次元が必要とされる。M理論の場合はさらに1つ、ヒモ自体に1つの次元が加えられます。
マイナスを消すための9次元
この宇宙に、隠れた空間次元があるかもしれないと考えたカルツァが、五次元宇宙における一般相対性理論の方程式を導出した時、修正された定式でも、3つの次元に関する方程式は本質的にアインシュタインの同じです。しかし新たな空間次元のために追加された方程式は、マクスウェルの電力を記述した方程式と同じものに見えました。そしてカルツァの理論から、重力も電磁気も空間の織物に起こる波と結びついているもの、重力は三空間に起こる波に、電気は巻き上げられ隠れた次元にからんだ波に運ばれるというような世界観が推測できました。しかしこの理論は、理論から予測される電子に関する情報が、観測データと矛盾していたために、捨てられ、超対称性理論の研究の時代まで、ほぼ忘れられていたでした。
超ヒモ理論にも、隠れた高次元が必要でした。
量子力学を組み込んだ宇宙では、ある出来事を完璧な精度で予測することはできません。ただし、確率予測は必ず0~1(つまり0~100%)の範囲に収まるとも言えます(単に直感的にでも、100%より高い確率とか、0%より低い確率とかというのはおかしい)。ヒモ理論は、量子力学と一般相対性理論を合わせた時に出る、高すぎる確率を排除しましたが、最初の理論では、逆にマイナスの確率が出現してしまっていました。そして、そのマイナスを消す計算にどうしても(ヒモが振動できる)さらなる高次元が必要だった。計算的には、ヒモが9つの独立した空間次元で振動するものなら、マイナス確率は消えてくれます。
カラビ-ヤウ図形の穴の数

理論の重要な点として、ヒモの振動パターンを縛る要素があります。
ヒモが動く時、隠れた次元の幾何学的形状は、共振振動パターンにかなり影響を与えると考えられています。そのことはつまり、(それらはヒモの振動パターンなため)素粒子の質量や力荷は、隠れた次元の大きさと幾何学的な形で決まることを示唆しています。1984年に、カンデラス(Philip Candelas)、ホロウィッツ(Gary Horowitz)、ストロミンジャー(Andrew Eben Strominger)、ウィッテンは、一組の六次元機何学図形が、ヒモ理論の条件を満たすことを証明しましたが、それこそカラビ-ヤウ空間(カラビ-ヤウ図形)だったのです。つまり隠された次元の形状は、この図形のパターン数(数万ほど)まで減らされることになりました。素粒子ヒモも、隠れた六次元も小さすぎて、現代の我々には確認することができません。ウィッテンらは、隠れた次元がカラビ-ヤウ図形として巻き上げられていることから、ヒモ側の振動パターンに関しても、いくつかの予測をしました。一般的に素粒子は、構成は同一だが質量の異なる3族に分類できるが、ヒモ理論以前は、なぜ族があるのかも、3つあるのかも謎でしかなかったのです。典型的カラビ-ヤウ図形には、ドーナツのそれと似ているとされる穴を有する。そして高次元カラビ-ヤウ図形では穴(それ自体が多次元構造)のパターンも様々。ウィッテンらは、空間のカラビ-ヤウ部分の穴がそれぞれ、エネルギーが最低のヒモ振動の族と結びついていることを見いだしました。知られる素粒子のパターンは、穴のパターンに対応します。つまりヒモの振動パターンの族数は、そのまま巻き上げられたカラビ-ヤウ図形の穴の数と等しいはずです。族の数は、隠れた次元の形状に見られる穴の数なのです。
現状では、素粒子に3族しか知られていないことは、隠れた次元の穴が3つというより、最低3つということを意味しているだけかもしれません。もし(まだ見つかっていませんが)何かの方法で、隠れた次元のカラビヤウの形をある程度特定することができたとしたら、その時に穴の数が3つであったならば、現状の観測データと一致するということになるでしょう。またヒモ理論においては、素粒子の各族の質量は、カラビ-ヤウ図形のさまざまな多次元の穴5境界の繋がり方によるとされています(これは直感的には、よりイメージしにくい)。それと、カラビ-ヤウ図形のパターンの中には、いくつか巻き方とほどけ方に関する特殊な幾何学的性質を有するものがあり、その特殊な性質の影響のために、ヒモの振動パターンが(現在では全く知られていない)特異的なパターンを発生させる可能性があるといいます。それはようするに、5分の1とか11分の1といった、半端な数の電荷の値なのです。仮にヒモ理論が正しくても、このような電荷値が存在しないことはありえますが、点粒子の理論に、このような数値の電荷を自然に組み込むことは難しいとされているので、もしこういったものが発見されたなら、ヒモ理論の強い根拠となるとも言われています。
巻きつきと振動。二重性の宇宙
ヒモ宇宙のみの動き
一般相対性理論的には、宇宙の湾曲した性質は、曲がった空間を記述するリーマン幾何学で考えられます。しかし最小のスケールを決定するヒモ理論においては、そのような幾何学は大きなスケールにおいてのみ成立します。ヒモ、プランク長さくらいのスケールではどうなるのでしょうか。
仮にこの宇宙が二次元空間の宇宙として、それでも、宇宙の膨張が止まって、収縮に転じ、最終的に最小の極限、つまりビッグクランチに到達することは考えられます。こうした宇宙の崩壊の時、とても小さな特異点という(多分)必然において、点かヒモかで異なるだろう小さなスケールでの幾何学が、見えてくるはずです。二次元宇宙の中で、点粒子もヒモ粒子も「空間の中を移動する」という運動をおこなうことができます。ただしループする素粒子ヒモは、空間を移動しながら振動し、その振動により質量や力荷が生じます。そしてもう1つ重要なことがあります。例えば二次元の宇宙が細長い時、ヒモは点と違い、宇宙の環状部分に巻きつくことができる。このヒモ独自の巻かれた状態は「巻きつきモード(Winding Mode)」と呼ばれます。巻きつきモードのヒモは、そのまま滑りながら振動するとされています。巻かれたヒモの最小の長さは、環状の次元の周囲の長さと、ヒモがそれを何周しているかと関連します。そのヒモの長さは、ヒモの最小質量と関連する。つまり、ヒモが長いほど質量は大きいのです。円周は半径に比例します。つまり最小限の巻きつきモードのヒモ質量も、巻きついた円の半径に比例します。質量とエネルギーはアインシュタインのE=mc^2で等価的に考えらます。すなわち巻かれたヒモのエネルギーは、環状の次元の半径に比例すると考えられるのです。巻かれていないヒモにももちろん最小限の長さがありますが、量子力学の効果がおそらくその質量を打ち消せます。よって、巻かれていないヒモは質量ゼロの素粒子(光子やグラビトン)として考えられるのです。
物理的区別ができない幾何学的に異なるはずの宇宙
1984年、吉川圭二(1935~2013)と山崎真見が、巻きつきモードが、ヒモが巻きついた次元の幾何学的性質にどう影響するかを見いだしました。それは驚くべき世界観だったのです。ヒモが巻きついた二次元宇宙の環状次元半径がプランク長さにまで縮んだ場合、ヒモ理論によると、環状次元半径がプランク長さよりも短い縮んでいく二次元宇宙と、環状次元半径がプランク長さよりも長い拡がっていく二次元宇宙は、物理プロセスが完全に同一らしいのです。つまりは、環状次元がプランク長さ以下に潰れようとする時、さらに潰れるはずの宇宙は、巻きつくヒモの幾何学の変化のために、逆に膨張するのかもしれない。変化の、つまり収縮が膨張へと転じるそのポイントこそが、プランク長さ、つまりヒモの最小スケールとなるのです。ヒモの宇宙では、エネルギーの起源は、振動と巻きつきという2つに種類分けできる。ヒモの振動も、力荷などを決める普通の振動と、ヒモ自体が位置を移動する一様な運動の振動の組み合わせですが、 これら(普通振動と一様振動)も分けて考えることができま。空間次元が小さいほど、ヒモは狭い範囲に収まるから、量子力学の不確定性原理の影響により、ヒモの一様運動のエネルギーは増えます。つまり環状次元なら、ヒモの一様振動エネルギーは環状次元の半径に反比例します。一方で環状次元に巻きつきモードのヒモのエネルギーは、半径に正比例します。巻かれたヒモの最小限の長さ(最小限のエネルギー)が、半径に比例するからです。つまり、半径が大きければ巻きつきエネルギーが大きく、一様振動エネルギーが小さくなる。半径が小さければ巻きつきエネルギーが小さく、一様振動エネルギーが大きくなるということになります。しかし普通振動はどう考えるべきか。実は普通振動は、環状次元の半径には左右されないことが示されています。
ようするに、等価的な2つの宇宙を推測できる。
大きな環状次元の宇宙と、小さな環状次元の宇宙。片方のヒモの巻きつきエネルギーは、もう一方のヒモの一様振動エネルギーに等しい。さらに普通振動の影響はどちらの宇宙でも同じです。つまりヒモの総エネルギーは2宇宙で同じ。そして共有されるのはヒモのエネルギー量だけではありません。あらゆる物理的性質が(ヒモ理論でそう考えるように)ヒモの総エネルギーにのみ影響されるなら、幾何学的に別の形(つまりスケールの異なるはずの)これらの2宇宙は、物理的に区別できません(「高い巻きつきエネルギー/低い振動エネルギー」と「低い巻きつきエネルギー/高い振動エネルギー」の2宇宙で、物理的な区別がつかないパターンが常にある)。これらの宇宙で行うどんな物理的実験も、その結果は一致します。
距離とは何か?
物理的に同じだが、異なるスケールの(つまり幾何学的には異なるはずの)2つの宇宙は何を意味しているのか。仮にこの宇宙が二重性という性質を持っていて、常に2つの宇宙のどちらも存在しているというのなら、我々は明らかに片方しか認識してないことになります。そして普通に考えるなら、我々が認識している宇宙は、巻きつきエネルギーが高く、振動エネルギーが低い方の宇宙です。そして、この等価性の2宇宙という世界観は、環状次元が6つあろうと変わりません。しかし宇宙に本当に二重性があるなら、ヒモが最初の大きさのはずの宇宙は、奇妙なことになるかもしれないのです。この宇宙が環状として、我々が認識しているほうのこの宇宙の半径がRとすると、もう一方の宇宙の半径は1/Rである。もちろんこれはとてつもなく小さい。プランク長さよりもはるかにです。この宇宙が膨張するということは、Rが大きくなるということだから、当然もう一方の宇宙はさらに小さくなっていくのです。
「距離とは何か?」と言うとまるで哲学的な問いのようですが、ひも理論の研究者たちは、この問いを今一度真剣に考えなければならなくなったのです。1988年、ロバート・ ブランデンバーガー(Robert H. Brandenberger)とカムラン・ヴァーファ(Cumrun Vafa)は、ある次元の空間的形が環状なら、距離というものには、2つの操作的な定義がありうるとしました。ある探査体が一定速度でどのくらい進めるのかを基準とした距離。2つの距離の違いは用いる探査体の違いであり、点粒子の世界観ではそのような異なる探査体はない。それらは(その異なる探査体とは)つまり、環状次元に巻きついていないヒモか、巻きついているヒモかということになります。実際的には距離だけではない。ヒモ宇宙だからこそありえる、反比例する物理要素は、つまりあらゆる物理要素です。問題は、おそらく現在の宇宙がそうであるように、一方のRが極端に大きいと(つまり1/Rが極端に小さいと)、我々が用いる探査体(自由ヒモか、巻きつきヒモ)の使いやすさにものすごく差が生じる。 我々は何も知らず利用しやすい頬のばかりを用いていたから、これまで2つの基準の一方にしか気づかなかったのかもしれない訳である。二重性の宇宙では、ヒモ自体が最小の大きさであるとは、つまり、我々のような存在にとって容易な基準のスケールの最小がヒモ、つまりプランク長さということであり、この見方を用い続ければ、さらに小さな宇宙を考えることもできるはずです。だがそうなると、もう一方の宇宙の方が、今度は我々(あるいはそ時に存在している何か)にとって馴染み深くなるでしょう。(そして、我々が従来考えてきたような距離の概念も、おそらくスイッチする。よって、最小のヒモのおかげで避けることができたあらゆる物理的問題が、再び問題として復活することもありません)
ミラー対称性の発見
しかし空間次元が環状でなくても、距離の概念がスイッチする二重性の宇宙というような、ヒモ理論の世界観は成り立つのでしょうか。この世界観で重要なことは、巻きつきモードという、まず(空間の形に関係なく)点粒子には絶対にありえない状態。実際問題、そうした巻きつきモードを可能とするなら、おそらく次元の形がどうであれ、等価な2宇宙という世界観は変わりません。ただし、巻きつきモードを安定させない空間次元の形はありうるのです。
(例えば球面なら、巻きついたヒモがずり落ちることが考えられるかもしれませんね)
ヒモ理論で、半径Rの円と、半径1/Rの円が物理的に区別できません。1980年代後半のディクソン(Lance Jenkins Dixon)以降、レルヒェ(wolfgang lerche)、ワーナー(Nicholas Warner)、ヴァーファといった物理学者たちは、対称性を意識した議論から、ある推測を示した。つまり、巻き上げられた次元の形について、異なる2つのカラビ-ヤウ図形が生み出す物理も、同一であるかもしれないと考えました。ヒモ粒子の族の数は、カラビ-ヤウ図形の穴の総数と関連し、個々の次元の穴の数とは関係ない。そこで個の次元の穴の数はちがうが総数は同じ2つのカラビ-ヤウ多様体(空間)は、形は違うが、同数の族を生じさせると考えらました。しかし彼らの推測は、2つのカラビ-ヤウのあらゆる物理的特性が一致することがありうるというものです。その後の、ウィッテン、グリーン(Brian Randolph Greene)、プレーサー(Ronen Presser)などの研究も合わさり、あるカラビ-ヤウ空間を数学的に操作して、別のカラビ-ヤウ空間を作る方法を開発しましたが、最初の図形と新図形とでは、奇数次元の穴の数と偶数次元の穴の数が入れかわっていたといいますう。どころか2つの異なるカラビ-ヤウ図形は、粒子の族の数以外の物理的特性も一致するかもしれないと、グリーンとプレッサーは見いだします。グリーンとプレッサーは、カラビ・ヤウ多様体と、ゲプナー・モデル(Gepner models)と呼ばれるある種の「共形場理論(Conformal Field Theory。CFT)」との関係を研究し、2つのカラビ-ヤウ空間の物理的対称性に気づきました。共形場理論とは、つまり空間の1点で交わる2曲線の接線のなす角度が保存されるような変換を利用し、不変な物理系を記述する理論です。また、カンデラス、リンカー(Monika Lynker)、シンムリック(Rolf Schimmrigk)の、多数のカラビ・ヤウ多様体サンプルの研究も、同じ推測を示唆しました。彼らが発見したのは、つまり幾何学的に異なる、ある2種のカラビ・ヤウ空間の「ミラー対称性(Mirror symmetry)」です。
(厳密には、文字通りに鏡に写した場合の対象性とは異なるはずでしたが、イメージ的にこのように名付けられました)
この、カラビ-ヤウに関する物理学者等の研究成果が、1991年、カリフォルニア州バークレーの数理科学研究所 (MSRI) で開催された会議で発表された時、会議に参加していた数学者の多くが、すでにより数学的に厳密な方法で示された別の結果と矛盾するために、それが間違っていると考えたといいます。しかし結局、コンピューターのプログラムでミスをしていたのは数学者たちの方で、ミラー対称性は純粋数学的なカラビ-ヤウ図形の研究にも便利なツールとなったから、これは、物理学者が純粋な数学の研究に貢献するという、(少なくともそれまでから考えると)珍しい結果となりました。
11つめの次元の謎
無限のダイアグラムをどう使うか
ヒモ理論の分析は、基本的に全て「摂動論(perturbation)」を用いています。摂動論とは、答を出せそうな要素の計算結果を、最初に無視した他の要素に関する修正を加えていくことで、複雑な問題の近似的答を導出する方法です。そうして出てくる近似的な答が、実際どれくらい近似的であるかということは、非常に重要な問題なのです。ヒモ理論の物理は、振動する各素粒子ヒモの(ヒモループの分裂や接合といった)相互作用から成り立ちます。さらに量子力学効果は、「仮想ヒモ対」とも呼ばれる、現れては消滅するヒモ/反ヒモの対(反対の振動パターンを示す2本のヒモ)も(ヒモの相互作用に影響を与える)宇宙の要素にします。ダイアグラムと呼ばれる、ヒモの空間での振る舞いを幾何学的に示した図を数学的に分析し、ある時空領域内での仮想ヒモ対の影響を探れると考えられています。しかし仮想ヒモの発生は、その時々によっていくらでも起こりうのです。つまり、2本のヒモの相互作用を探るためのダイアグラムのパターンは、仮想ひも対がないダイアグラム、仮想ヒモ対1組のダイアグラム、仮想ひも対2組のダイアグラムと、いくつもあり、それら全てを足し合わせることが有効だとされています。しかし実質無限にあるようなダイアグラム群を全て足し合わせることは不可能です。ヒモ理論研究者のアプローチは理にはかなっているが、かなり妥協があることも確かなのです。つまり、仮想ループなしパターンが、わりと正確な見積もりであること、さらに仮想ループの数が増えるほど修正量が小さくなることを期待するというもの。そして、量子ゆらぎで1本のヒモが2本に分かれ、仮想対が一瞬現れる可能性を決める数が、「ヒモ結合定数」と呼ばれるものです。ヒモ結合定数は、もとのヒモループと、わかれてできる2仮想ループの量子効果の関連の強さ、つまりは互いにどんな強さで結合しているかを示します。ようするにヒモ結合定数が大きいほど、ヒモは2つにわかれやすく(後にも2つが結合しやすい)、結合定数が小さいほど仮想ヒモが発生しにくい。つまり結合定数が小さいことは、ダイアグラムの従来の摂動的アプローチが有効でありやすいことを示唆しています。5つのヒモ理論の、結合定数の大小によるスイッチが重要だったのはそういう理由だったのです。しかし、実際この宇宙のヒモ結合定数の値がいくらであるのかについては、どんな場合においてもわかっていません。しかしヒモ結合定数の値が、ヒモのさまざまな振動パターンに重要な影響力を有するだろうことは確かとされるいます。(だからこれは、ヒモ理論における非常に重要な未解決問題とされているのです)
ヒモ自体の次元は、空間次元とは異なるか
「ヒモ理論95会議」でウィッテンは、ⅡA型ひも理論から出発して、結合定数を1以上に大きくしていけば、分析できると思われる物理学は、低エネルギーで11次元超重力によって近似されると主張しました。後にウィッテンとホジャヴァ(Petr Hořava)は、ヘテロE理論において、強く結合したヘテロE理論にも、11次元の記述があることを見いだしました。結合定数が大きくなった時に現れる新しい次元というのは、おそらく誰ひとり予想できなかった展開でした。ヒモの構造は、結合定数が大きくなると、一次元のループだったものが引き伸ばされ、二次元の構造となります。しかしヒモの二次元構造は、結合定数が小さい場合、ものすごく小さく圧縮され、実質一次元のヒモとして扱えます。それが1次元ヒモと認識されてしまったことは当然かもしれません。5つのヒモ理論が個別にしか研究されていなかった頃は、結合定数が大きなパターンというのは、ほとんど考えられない問題だったのです。しかし、このヒモ自体の次元とは何なのか。前の隠れた6次元は、ヒモの動作と、それによる物理的な結果のために想定された、ヒモが動く空間です。新たな次元は、ヒモ自体の有する何かということになります。
5つの宇宙をつなぐ鍵としての二重性
ヒモ宇宙における巻きつきモードと振動モードのスイッチは、5つのヒモ理論の双対性とも関連しています。巻きつきモードと振動モードを入れかえ、半径Rの環状次元の宇宙の記述を、半径1/Rの環状次元の宇宙の記述に変換(スイッチ)する場合、それが実はⅡA型ヒモ理論とⅡB型ヒモ理論、また、ヘテロOヒモ理論とへテロEヒモ理論のスイッチにもなります。ようするに、半径Rの環状次元宇宙のⅡA型ヒモ理論物理は、半径1/Rの環状次元宇宙のⅡB型ヒモ理論の物理と同一なのです(ヘテロOとヘテロEにも同じことが言える)。結合定数の大小の双対性と合わせると、5つのヒモ理論をまとめる網の理論。すなわちM理論が見えてきます。だがMが意味することの1つ、11番目の次元、ヒモの膜については、現在までずっと、全く解けそうにない謎のままなのです。
ブラックホール=素粒子?
ブラックホールらしき天体は、宇宙にいくつも観測されています。この不可思議な天体をヒモ理論は、どのように説明するのでしょうか?実はけっこう普通な説明がされています。(出来る可能性がある)
鍵は、ブラックホールと素粒子の類似性である。
ブラックホールの内部では、その中に取り込まれるまでに、どんな物であったものも、全て等しく完全破壊されていると考えられている。つまりブラックホールの一部であるまでの事は関係なく、ブラックホールになってしまうと、後はただブラックホール。せいぜい残る情報は質量くらいである。つまり素粒子と似たような感じなのである。そういうわけで、「ブラックホールは巨大な素粒子」というアイデアはわりと昔からあるのですが、ヒモ理論は見事にその考えを取り込みます。ヒモ理論モデルでは、宇宙には折り畳まれた六次元、カラビヤウ空間が、敷き詰められているはずだが、そのカラビヤウ空間は、引き裂かれた場合に、自動修復し、また別の型のカラビヤウ空間になるという計算結果があります。ヒモ理論の宇宙でのブラックホールの内部ではまさにそれが起こっているとされています。カラビヤウ空間は裂け、しかしまた別のカラビヤウ空間となる。そうして変化したカラビヤウ空間の中には、計算上、なんと周囲の質量を0にしてしまうものがあり、つまりヒモ理論宇宙では、「質量0のブラックホール」というのが存在する事になるのです。その質量0のブラックホールを、質量0の素粒子だと解釈すれば、まったく自然に思えるシナリオが浮かび上がります。つまりブラックホールはやがて、素粒子に転移する。考えようによっては、特異点も回避出来ると思われます。中心問題を回避したように。
最後に
とまあ、物理における現代の歴史を少々綴った訳ですが、多分読んだ方は訳の分からないことになっていると思います(笑)。僕はそれで良いと思っています。決して無理をなさらずに!。世の中が分からないことだらけなように、宇宙も分からないことだらけです。でも我々人間は知恵という能力を獲得しています。「知りたいのは人間の本質」という知識欲がある限り「知りたい」という追求は続くのでしょう。と同時に最新の物理学でSF小説を執筆することが如何に大変かも記事を書いていて思ったことです。普通であれば理解するのにそれ相応の期間が掛かります。それを解釈しながらSFの世界に反映するのですから「三体」が面白いのは当然と言えますね。
さあ、SFを楽しみましょう!!


